متكامل

التكامل هو عملية الاشتقاق العكسية.

تكامل الدالة هو المنطقة الواقعة أسفل الرسم البياني للوظيفة.

تعريف متكامل غير محدد

متى dF (x) / dx = f (x) =/ متكامل (f (x) * dx) = F (x) + c

خصائص تكاملية غير محددة

تكامل (f (x) + g (x)) * dx = تكامل (f (x) * dx) + تكامل (g (x) * dx)

متكامل (a * f (x) * dx) = a * لا يتجزأ (f (x) * dx)

متكامل (f (a * x) * dx) = 1 / a * F (a * x) + c

تكامل (f (x + b) * dx) = F (x + b) + c

متكامل (f (a * x + b) * dx) = 1 / a * F (a * x + b) + c

تكامل (df (x) / dx * dx) = f (x)

تغيير متغير التكامل

متىس = ز (ر) وdx = g '(t) * dt

متكامل (f (x) * dx) = متكامل (f (g (t)) * g '(t) * dt)

تكامل اجزاء

متكامل (f (x) * g '(x) * dx) = f (x) * g (x) - متكامل (f' (x) * g (x) * dx)

جدول التكاملات

تكامل (f (x) * dx = F (x) + c

متكامل (أ * دكس) = أ * س + ج

متكامل (x ^ n * dx) = 1 / (a ​​+ 1) * x ^ (a + 1) + c ، عندما تكون a </ - 1

التكامل (1 / x * dx) = ln (abs (x)) + c

تكامل (e ^ x * dx) = e ^ x + c

متكامل (a ^ x * dx) = a ^ x / ln (x) + c

متكامل (ln (x) * dx) = x * ln (x) - x + c

التكامل (sin (x) * dx) = -cos (x) + c

التكامل (cos (x) * dx) = sin (x) + c

تكامل (tan (x) * dx) = -ln (abs (cos (x))) + c

متكامل (arcsin (x) * dx) = x * arcsin (x) + sqrt (1-x ^ 2) + c

متكامل (arccos (x) * dx) = x * arccos (x) - sqrt (1-x ^ 2) + c

متكامل (arctan (x) * dx) = x * arctan (x) - 1/2 * ln (1 + x ^ 2) + c

متكامل (dx / (ax + b)) = 1 / a * ln (abs (a * x + b)) + c

متكامل (1 / sqrt (a ^ 2-x ^ 2) * dx) = arcsin (x / a) + c

تكامل (1 / sqrt (x ^ 2 + - a ^ 2) * dx) = ln (abs (x + sqrt (x ^ 2 + - a ^ 2)) + c

متكامل (x * sqrt (x ^ 2-a ^ 2) * dx) = 1 / (a ​​* arccos (x / a)) + c

متكامل (1 / (a ​​^ 2 + x ^ 2) * dx) = 1 / a * arctan (x / a) + c

متكامل (1 / (a ​​^ 2-x ^ 2) * dx) = 1 / 2a * ln (abs (((a + x) / (ax))) + c

التكامل (sinh (x) * dx) = cosh (x) + c

تكامل (cosh (x) * dx) = sinh (x) + c

تكامل (tanh (x) * dx) = ln (cosh (x)) + c

 

تعريف متكامل محدد

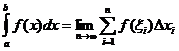
متكامل (a..b، f (x) * dx) = lim (n-/ inf، sum (i = 1..n، f (z (i)) * dx (i))) 

متىس 0 = أ ، س = ب

دس (ك) = س (ك) - س (ك -1)

س (ك -1) <= ض (ك) <= س (ك)

حساب متكامل محدد

متى 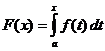و

 dF (x) / dx = f (x) و

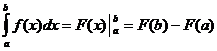
متكامل (أ..ب ، و (س) * دكس) = و (ب) - و (أ) 

خصائص متكاملة محددة

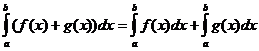
متكامل (a..b، (f (x) + g (x)) * dx) = متكامل (a..b، f (x) * dx) + متكامل (a..b، g (x) * dx )

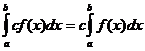
متكامل (a..b ، c * f (x) * dx) = c * متكامل (a..b ، f (x) * dx)

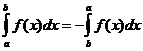
متكامل (a..b، f (x) * dx) = - متكامل (b..a، f (x) * dx)

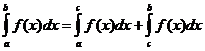
متكامل (a..b، f (x) * dx) = متكامل (a..c، f (x) * dx) + متكامل (c..b، f (x) * dx)

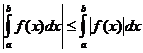
القيمة المطلقة (تكامل (a..b ، f (x) * dx)) <= متكامل (a..b ، abs (f (x)) * dx)

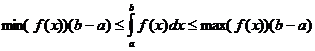min (f (x)) * (ba) <= متكامل (a..b، f (x) * dx) <= max (f (x)) * (ba) متىx عضو في [أ ، ب]

تغيير متغير التكامل

متىس = ز (ر) وdx = g '(t) * dt وز (ألفا) = أ وز (بيتا) = ب

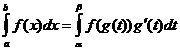
متكامل (a..b، f (x) * dx) = متكامل (alpha..beta، f (g (t)) * g '(t) * dt)

تكامل اجزاء

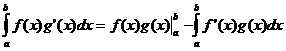
متكامل (a..b، f (x) * g '(x) * dx) = تكامل (a..b، f (x) * g (x) * dx) - تكامل (a..b، f' (x) * g (x) * dx)

يعني نظرية القيمة

عندما تكون f ( x ) متصلة ، توجد نقطةج عضو في [أ ، ب] وبالتالي

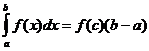
متكامل (a..b، f (x) * dx) = f (c) * (ba)  

تقريب شبه منحرف للتكامل المحدد

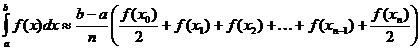
متكامل (a..b، f (x) * dx) ~ (ba) / n * (f (x (0)) / 2 + f (x (1)) + f (x (2)) + .. . + f (x (n-1)) + f (x (n)) / 2)

وظيفة جاما

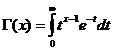
جاما (x) = متكامل (0..inf، t ^ (x-1) * e ^ (- t) * dt

دالة جاما متقاربة من أجل x/ 0 .

خصائص وظيفة جاما

G ( x +1) = x G ( x )

ز ( ن +1) = ن ! ، عندما ن ℕ (عدد صحيح موجب).عضو في

وظيفة بيتا

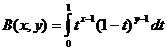
ب (س ، ص) = متكامل (0..1 ، تي ^ (ن -1) * (1-ت) ^ (ص -1) * دت

دالة بيتا وعلاقة دالة جاما

ب (س ، ص) = جاما (س) * جاما (ص) / جاما (س + ص)

 

 

 

حساب التفاضل والتكامل
جداول سريعة