دالة القوسين

arcsin (x) ، sin -1 (x) ، دالة الجيب العكسية .

تعريف Arcsin

يتم تعريف قوس جيب الزاوية لـ x على أنه دالة الجيب العكسية لـ x عند -1≤x≤1.

عندما يكون جيب y يساوي x:

الخطيئة ص = س

ثم قوس جيب الزاوية x يساوي دالة الجيب العكسية لـ x ، والتي تساوي y:

arcsin x = sin -1 x = y

مثال

arcsin 1 = sin -1 1 = π / 2 rad = 90 °

الرسم البياني لأركسين

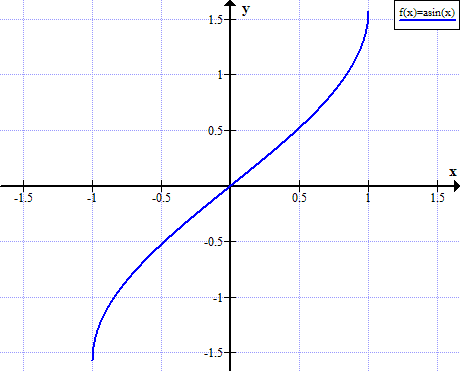
قواعد Arcsin

اسم القاعدة قاعدة
جيب القوسين الخطيئة (arcsin x ) = x
قوس الجيب الجيب arcsin (sin x ) = x +2 k π ، عندما k ∈ℤ ( k عدد صحيح)
Arcsin للحجة السلبية arcsin (- x ) = - arcsin x
زوايا متكاملة arcsin x = π / 2 - arccos x = 90 ° - arccos x
مجموع Arcsin arcsin α + arcsin ( β ) = arcsin ( α√ (1- β 2 ) + β√ (1- α 2 ) )
فرق Arcsin arcsin α - arcsin ( β ) = arcsin ( α√ (1- β 2 ) - β√ (1- α 2 ) )
جيب تمام القوس
ظل القوسين
مشتق من القوسين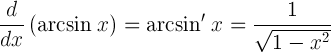
تكامل غير محدد من قوسين

جدول Arcsin

x قوسين (x)

(راد)

 قوسين (x)

(°)
-1 -π / 2 -90 درجة
-√ 3 /2 -π / 3 -60 درجة
-√ 2 /2 -π / 4 -45 درجة
-1/2 -π / 6 -30 درجة
0 0 0 درجة
1/2 / 6 30 درجة
√ 2 /2 π / 4 45 درجة
√ 3 /2 / 3 60 درجة
1 π / 2 90 درجة

 

أنظر أيضا

علم المثلثات
جداول سريعة