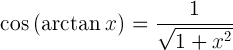دالة قوسية

Arctan (x) ، tan -1 (x) ، دالة الظل العكسي .

تعريف Arctan

يتم تعريف قوس ظل الزاوية لـ x على أنه دالة الظل العكسية لـ x عندما تكون x حقيقية (x ∈ℝ ).

عندما يكون ظل y يساوي x:

تان ص = س

إذن ، فإن قوس ظل الزاوية لـ x يساوي دالة الظل العكسية لـ x ، والتي تساوي y:

أركتان س = تان -1 س = ص

مثال

أركتان 1 = تان -1 1 = π / 4 راد = 45 درجة

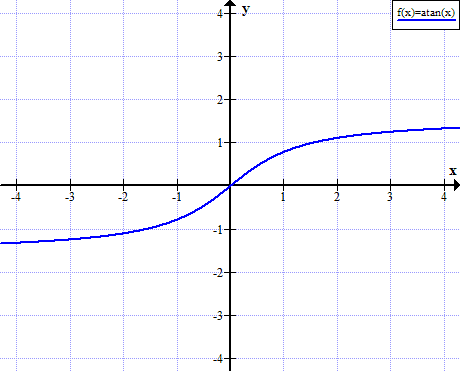
رسم بياني لأركتان

قواعد أركتان

اسم القاعدة قاعدة
ظل قوس ظل

تان (أركتان س ) = س
Arctan من الحجة السلبية

arctan (- x ) = - arctan x
مجموع أركتان

arctan α + arctan β = arctan [( α + β ) / (1- αβ )]
فرق أركتان

arctan α - arctan β = arctan [( α - β ) / (1+ αβ )]
جيب قوس ظل

جيب التمام من قوس ظل

حجة متبادلة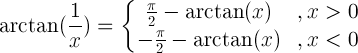
أركتان من أركسين
مشتق من arctan
تكامل غير محدد من arctan

طاولة أركتان

x أركتان (x)

(راد)

 أركتان (x)

(°)
-∞ -π / 2 -90 درجة
-3 -1.2490 -71.565 درجة
-2 -1.1071 -63.435 درجة
-√ 3 -π / 3 -60 درجة
-1 -π / 4 -45 درجة
-1 / 3 -π / 6 -30 درجة
-0.5 -0.4636 -26.565 درجة
0 0 0 درجة
0.5 0.4636 26.565 درجة
1 / √ 3 / 6 30 درجة
1 π / 4 45 درجة
√ 3 / 3 60 درجة
2 1.1071 63.435 درجة
3 1.2490 71.565 درجة
∞ π / 2 90 درجة

 

 

أنظر أيضا

علم المثلثات
جداول سريعة