Числа и последователност на Фибоначи

Последователността на Фибоначи е поредица от числа, където всяко число е сумата от предишните 2 числа, с изключение на първите две числа, които са 0 и 1.

• Формула за последователност на Фибоначи
• Конвергенция на златното сечение
• Таблица на последователността на Фибоначи
• Калкулатор на последователността на Фибоначи
• C ++ код на функцията на Фибоначи

Формула за последователност на Фибоначи

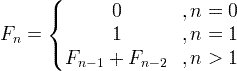
Например:

F ₀ = 0

F ₁ = 1

F ₂ = F ₁ + F ₀ = 1 + 0 = 1

F ₃ = F ₂ + F ₁ = 1 + 1 = 2

F ₄ = F ₃ + F ₂ = 2 + 1 = 3

F ₅ = F ₄ + F ₃ = 3 + 2 = 5

...

Конвергенция на златното сечение

Съотношението на две последователни числа на Фибоначи се сближава със златното сечение:

φ е златното съотношение = (1 + √ 5 ) / 2 ≈ 1,61803399

Таблица на последователността на Фибоначи

n	F n
0	0
1	1
2	1
3	2
4	3
5	5
6	8
7	13
8	21
9	34
10	55
11	89
12	144
13	233
14	377
15	610
16	987
17	1597
18	2584
19	4181
20	6765

Калкулатор на последователността на Фибоначи

TBD

C код на функцията на Фибоначи

double Fibonacci(unsigned int n)

{

    double f_n =n;

    double f_n1=0.0;

    double f_n2=1.0;

 

    if( n / 1 ) {

        for(int k=2; k<=n; k++) {

            f_n  = f_n1 + f_n2;

            f_n2 = f_n1;

            f_n1 = f_n;

        }

    }

 

    return f_n;

}