e константа

Константата или числото на Ойлер е математическа константа. Константата e е реално и ирационално число.

e = 2,718281828459 ...

Определение на д
Свойства на e
Основен e логаритъм
Експоненциална функция
Формулата на Ойлер

Определение на д

Константата e се определя като граница:

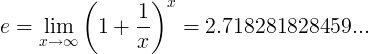
$e = \ lim_ {x \ rightarrow \ infty} \ ляво (1+ \ frac {1} {x} \ дясно) ^ x = 2.718281828459 ...$

Алтернативни дефиниции

Константата e се определя като граница:

$e = \ lim_ {x \ rightarrow 0} \ ляво (1+ \ дясно x) ^ \ frac {1} {x}$

Константата e се определя като безкраен ред:

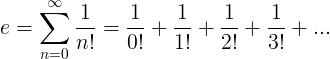
$e = \ sum_ {n = 0} ^ {\ infty} \ frac {1} {n!} = \ frac {1} {0!} + \ frac {1} {1!} + \ frac {1} { 2!} + \ Frac {1} {3!} + ...$

Свойства на e

Взаимно на д

Реципрочното на e е границата:

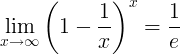
$\ lim_ {x \ rightarrow \ infty} \ вляво (1- \ frac {1} {x} \ вдясно) ^ x = \ frac {1} {e}$

Производни на д

Производната на експоненциалната функция е експоненциалната функция:

( e ^x ) '= e ^x

Производната на функцията на естествения логаритъм е реципрочната функция:

(log _e x ) '= (ln x )' = 1 / x

Интеграли на e

Неопределеният интеграл на експоненциалната функция e ^x е експоненциалната функция e ^x .

∫ e ^x dx = e ^x + c

Неопределеният интеграл от функцията за естествен логаритъм log _e x е:

∫ log _e x dx = ∫ ln x dx = x ln x - x + c

Определеният интеграл от 1 до e на реципрочната функция 1 / x е 1:

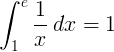
$\ int_ {1} ^ {e} \ frac {1} {x} \: dx = 1$

Основен e логаритъм

Естественият логаритъм на число x се дефинира като основен e логаритъм на x:

ln x = log _e x

Експоненциална функция

Експоненциалната функция се дефинира като:

f ( x ) = exp ( x ) = e ^x

Формулата на Ойлер

Комплексното число e ^iθ има идентичността:

e ^iθ = cos ( θ ) + i sin ( θ )

i е въображаемата единица (квадратен корен от -1).

θ е всяко реално число.