Нулев номер (0)
- Определение на нулев номер
- История на нулев номер
- Свойства на нулево число
- Комплекти, които съдържат нула
Определение на нулев номер
Нула е число, използвано в математиката, за да се опише никакво количество или нулево количество.
Когато на масата има 2 ябълки и вземем двете ябълки, можем да кажем, че на масата има нула ябълки.
Нулевото число не е положително число и не е отрицателно число.
Нулата е и цифра за заместване в други числа (например: 40, 103, 170).
Нула номер ли е?
Нулата е число. Това не е нито положително, нито отрицателно число.
Нулева цифра
Нулевата цифра се използва като заместител при писане на числа.
Например:
204 = 2 × 100 + 0 × 10 + 4 × 1
История на нулев номер
Кой е измислил нулевото число?
Съвременният символ 0 е изобретен в Индия през 6-ти век, използван по-късно от персите и арабите и по-късно в Европа.
Символ на нула
Нулевото число се обозначава със символа 0 .
Арабската цифрова система използва символа ٠.
Свойства на нулево число
x представлява произволно число.
| Операция | Правило | Пример |
|---|---|---|
Събиране |
x + 0 = x |
3 + 0 = 3 |
Изваждане |
x - 0 = x |
3 - 0 = 3 |
Умножение |
x × 0 = 0 |
5 × 0 = 0 |
Дивизия |
0 ÷ x = 0 , когато x ≠ 0 |
0 ÷ 5 = 0 |
| x ÷ 0 е неопределен |
5 ÷ 0 е недефинирано |
|
Степенуване |
0 x = 0 |
0 5 = 0 |
| x 0 = 1 |
5 0 = 1 |
|
Корен |
√ 0 = 0 |
|
Логаритъм |
log b (0) е недефиниран |
|
| |
||
Факториал |
0! = 1 |
|
Синус |
sin 0º = 0 |
|
Косинус |
cos 0º = 1 |
|
Допирателна |
тен 0º = 0 |
|
Производно |
0 '= 0 |
|
Неразделна |
∫ 0 d x = 0 + C |
|
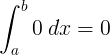 |
Нулево добавяне
Събирането на число плюс нула е равно на числото:
x + 0 = x
Например:
5 + 0 = 5
Нулево изваждане
Изваждането на число минус нула е равно на числото:
x - 0 = x
Например:
5 - 0 = 5
Умножение по нула
Умножение на число по нула е равно на нула:
x × 0 = 0
Например:
5 × 0 = 0
Число, разделено на нула
Деление на число на нула не е дефинирано:
x ÷ 0 е неопределен
Например:
5 ÷ 0 е недефинирано
Нула, разделена на число
Делението на нула на число е нула:
0 ÷ x = 0
Например:
0 ÷ 5 = 0
Брой до нулевата мощност
Степента на число, повдигнато с нула, е една:
x 0 = 1
Например:
5 0 = 1
Логаритъм от нула
Основният логаритъм b от нула е недефиниран:
log b (0) е недефиниран
Няма число, с което да вдигнем основата b, за да получим нула.
Само границата на основния b логаритъм от x, когато x сходи нула, е минус безкрайност:
![]()
Комплекти, които съдържат нула
Нулата е елемент от естествените числа, цели числа, реални числа и комплекси от комплексни числа:
| Комплект | Задайте нотация за членство |
|---|---|
| Естествени числа (неотрицателни) | 0 ∈ ℕ 0 |
| Цели числа | 0 ∈ ℤ |
| Реални числа | 0 ∈ ℝ |
| Комплексни числа | 0 ∈ ℂ |
| Рационални числа | 0 ∈ ℚ |
Нула четно или нечетно число?
Наборът от четни числа е:
{..., -10, -8, -6, -4, -2, 0, 2, 4, 6, 8, 10, ...}
Наборът от нечетни числа е:
{..., -9, -7, -5, -3, -1, 1, 3, 5, 7, 9, ...}
Нула е цяло число, кратно на 2:
0 × 2 = 0
Нула е член на зададените четни числа:
0 ∈ {2 k , k ∈ℤ}
Така че нулата е четно, а не нечетно число.
Нулата естествено число ли е?
Има две определения за естествените числа.
Наборът от неотрицателни цели числа:
ℕ 0 = {0,1,2,3,4,5,6,7,8, ...}
Наборът от положителни цели числа:
ℕ 1 = {1,2,3,4,5,6,7,8, ...}
Нула е член на набора от неотрицателни цели числа:
0 ∈ ℕ 0
Нула не е член на множеството положителни цели числа:
0 ∉ ℕ 1
Нула цяло число ли е?
Има три определения за целите числа:
Наборът от цели числа:
ℤ = {0,1,2,3,4,5,6,7,8, ...}
Наборът от неотрицателни цели числа:
ℕ 0 = {0,1,2,3,4,5,6,7,8, ...}
Наборът от положителни цели числа:
ℕ 1 = {1,2,3,4,5,6,7,8, ...}
Нула е член на множеството от цели числа и на множеството от неотрицателни цели числа:
0 ∈ ℤ
0 ∈ ℕ 0
Нула не е член на множеството положителни цели числа:
0 ∉ ℕ 1
Нулата е цяло число?
Наборът от цели числа:
ℤ = {0,1,2,3,4,5,6,7,8, ...}
Нула е член на набора от цели числа:
0 ∈ ℤ
Значи нулата е цяло число.
Рационално число ли е нулата?
Рационалното число е число, което може да бъде изразено като фактор на две цели числа:
ℚ = { n / m ; n , m ∈ℤ}
Нула може да се запише като част от две цели числа.
Например:
0 = 0/3
Така че нулата е рационално число.
Нула положително число ли е?
Положителното число се дефинира като число, което е по-голямо от нула:
x / 0
Например:
5/ 0
Тъй като нулата не е по-голяма от нула, това не е положително число.
Нула ли е просто число?
Числото 0 не е просто число.
Нулата не е положително число и има безкраен брой делители.
Най-ниското просто число е 2.