Funció Arccos (x)
Arccos (x), cos -1 (x), funció cosinus inversa .
Definició d’Arccos
L’arcosina de x es defineix com la funció de cosinus inversa de x quan -1≤x≤1.
Quan el cosinus de y és igual a x:
cos y = x
Aleshores l’arcosin de x és igual a la funció inversa del cosinus de x, que és igual a y:
arccos x = cos -1 x = y
(Aquí cos -1 x significa el cosinus invers i no significa cosinus a la potència de -1).
Exemple
arccos 1 = cos -1 1 = 0 rad = 0 °
Gràfic d'arcs
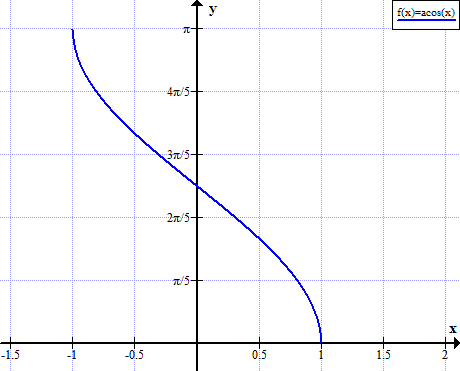
Regles Arccos
| Nom de la regla | Regla |
|---|---|
| Cosinus d’arcososina | cos (arccos x ) = x |
| Arccosine de cosinus | arccos (cos x ) = x + 2 k π, quan k ∈ℤ ( k és enter) |
| Arccos d'argument negatiu | arccos (- x ) = π - arccos x = 180 ° - arccos x |
| Angles complementaris | arccos x = π / 2 - arcsin x = 90 ° - arcsin x |
| Arccos suma | arccos ( α ) + arccos ( β ) = arccos ( αβ - √ (1- α 2 ) (1- β 2 ) ) |
| Arccos diferència | arccos ( α ) - arccos ( β ) = arccos ( αβ + √ (1- α 2 ) (1- β 2 ) ) |
| Arccos de pecat de x | arccos (sin x ) = - x - (2 k +0,5) π |
| Seno d'arcosina | |
| Tangent de l’arcosina |  |
| Derivat d'arcosina | 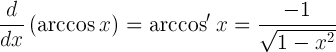 |
| Integral indefinida d'arcosina | |
Taula Arccos
| x | arccos (x) (rad) |
arccos (x) (°) |
|---|---|---|
| -1 | π | 180 ° |
| -√ 3 /2 | 5π / 6 | 150 ° |
| -√ 2 /2 | 3π / 4 | 135 ° |
| -1/2 | 2π / 3 | 120 ° |
| 0 | π / 2 | 90 ° |
| 1/2 | π / 3 | 60 ° |
| √ 2 /2 | π / 4 | 45 ° |
| √ 3 /2 | π / 6 | 30 ° |
| 1 | 0 | 0 ° |
Vegeu també
- Funció cosinus
- Funció Arcsine
- Funció Arctan
- Calculadora Arccos
- Convertidor de radians a graus
- Arccos de 0
- Arccos d'1
- Arccos de 2
- Arccos de 3
- Arccos de cos
- Arccos del pecat
- Derivat arccos
- Gràfic Arccos
- Cos d'arcs
- Pecat d'arcs
- Tan d'arcs