Kvadratická rovnice
Kvadratická rovnice je polynom druhého řádu se 3 koeficienty - a , b , c .
Kvadratická rovnice je dána vztahem:
sekera 2 + bx + c = 0
Řešení kvadratické rovnice je dáno 2 čísly x 1 a x 2 .
Můžeme změnit kvadratickou rovnici na formu:
( x - x 1 ) ( x - x 2 ) = 0
Kvadratický vzorec
Řešení kvadratické rovnice je dáno kvadratickým vzorcem:
![]()
Výraz uvnitř druhé odmocniny se nazývá diskriminační a je označen Δ:
Δ = b 2 - 4 stříd
Kvadratický vzorec s diskriminační notací:
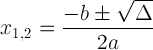
Tento výraz je důležitý, protože nám může říci o řešení:
- Když Δ/ 0, existují 2 skutečné kořeny x 1 = (- b + √ Δ ) / (2a) a x 2 = (- b-√ Δ ) / (2a) .
- Když Δ = 0, existuje jeden kořen x 1 = x 2 = -b / (2a) .
- Když Δ <0, neexistují žádné skutečné kořeny, existují 2 komplexní kořeny:
x 1 = (- b + i√ -Δ ) / (2a) a x 2 = (- bi√ -Δ ) / (2a) .
Problém č. 1
3 x 2 +5 x +2 = 0
řešení:
a = 3, b = 5, c = 2
x 1,2 = (-5 ± √ (5 2 - 4 × 3 × 2)) / (2 × 3) = (-5 ± √ (25-24)) / 6 = (-5 ± 1) / 6
x 1 = (-5 + 1) / 6 = -4/6 = -2/3
x 2 = (-5 - 1) / 6 = -6/6 = -1
Problém č. 2
3 x 2 -6 x 3 = 0
řešení:
a = 3, b = -6, c = 3
x 1,2 = (6 ± √ ((-6) 2 - 4 × 3 × 3)) / (2 × 3) = (6 ± √ (36-36)) / 6 = (6 ± 0) / 6
x 1 = x 2 = 1
Problém č. 3
x 2 + 2 x +5 = 0
řešení:
a = 1, b = 2, c = 5
x 1,2 = (-2 ± √ (2 2 - 4 × 1 × 5)) / (2 × 1) = (-2 ± √ (4-20)) / 2 = (-2 ± √ (-16 )) / 2
Neexistují žádná skutečná řešení. Hodnoty jsou komplexní čísla:
x 1 = -1 + 2 i
x 2 = -1 - 2 i
Graf kvadratické funkce
Kvadratická funkce je polynomiální funkce druhého řádu:
f ( x ) = sekera 2 + bx + c
Řešení kvadratické rovnice jsou kořeny kvadratické funkce, což jsou průsečíky grafu kvadratické funkce s osou x, když
f ( x ) = 0
Když existují 2 průsečíky grafu s osou x, existují 2 řešení kvadratické rovnice.
Když je 1 průsečík grafu s osou x, existuje 1 řešení kvadratické rovnice.
Když neexistují žádné průsečíky grafu s osou x, nedostaneme reálná řešení (nebo 2 komplexní řešení).