Pravidla logaritmu
Základna b logaritmus řady je exponent , že musíme zvýšit základnu s cílem získat telefonní číslo.
- Definice logaritmu
- Logaritmická pravidla
- Problémy logaritmu
- Složitý logaritmus
- Graf protokolu (x)
- Logaritmická tabulka
- Logaritmická kalkulačka
Definice logaritmu
Když je b zvýšeno na sílu y je rovno x:
b y = x
Pak se základní b logaritmus x rovná y:
log b ( x ) = y
Například když:
2 4 = 16
Pak
log 2 (16) = 4
Logaritmus jako inverzní funkce exponenciální funkce
Logaritmická funkce,
y = log b ( x )
je inverzní funkce exponenciální funkce,
x = b y
Pokud tedy spočítáme exponenciální funkci logaritmu x (x/ 0),
f ( f -1 ( x )) = b log b ( x ) = x
Nebo pokud vypočítáme logaritmus exponenciální funkce x,
f -1 ( f ( x )) = log b ( b x ) = x
Přirozený logaritmus (ln)
Přirozený logaritmus je logaritmus k základnímu e:
ln ( x ) = log e ( x )
Když e konstanta je číslo:
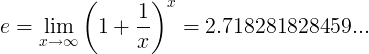
nebo
![]()
Viz: Přirozený logaritmus
Výpočet inverzního logaritmu
Inverzní logaritmus (nebo anti logaritmus) se vypočítá zvýšením základny b na logaritmus y:
x = log -1 ( y ) = b y
Logaritmická funkce
Logaritmická funkce má základní formu:
f ( x ) = log b ( x )
Logaritmická pravidla
| Název pravidla | Pravidlo |
|---|---|
Logaritmické pravidlo produktu |
log b ( x ∙ y ) = log b ( x ) + log b ( y ) |
Pravidlo kvocientu logaritmu |
log b ( x / y ) = log b ( x ) - log b ( y ) |
Logaritmické pravidlo síly |
log b ( x y ) = y ∙ log b ( x ) |
Logaritmické pravidlo základního přepínání |
log b ( c ) = 1 / log c ( b ) |
Logaritmické základní pravidlo změny |
log b ( x ) = log c ( x ) / log c ( b ) |
Derivace logaritmu |
f ( x ) = log b ( x ) ⇒ f ' ( x ) = 1 / ( x ln ( b )) |
Integrál logaritmu |
∫ log b ( x ) dx = x ∙ (log b ( x ) - 1 / ln ( b ) ) + C |
Logaritmus záporného čísla |
log b ( x ) není definováno, když x ≤ 0 |
Logaritmus 0 |
log b (0) není definován |
Logaritmus 1 |
log b (1) = 0 |
Logaritmus základny |
log b ( b ) = 1 |
Logaritmus nekonečna |
lim log b ( x ) = ∞, když x → ∞ |
Viz: Pravidla logaritmu
Logaritmické pravidlo produktu
Logaritmus násobení x a y je součtem logaritmu x a logaritmu y.
log b ( x ∙ y ) = log b ( x ) + log b ( y )
Například:
log 10 (3 ∙ 7) = log 10 (3) + log 10 (7)
Pravidlo kvocientu logaritmu
Logaritmus rozdělení x a y je rozdíl logaritmu x a logaritmu y.
log b ( x / y ) = log b ( x ) - log b ( y )
Například:
log 10 (3 / 7) = log 10 (3) - log 10 (7)
Logaritmické pravidlo síly
Logaritmus x zvýšený na sílu y je y krát logaritmus x.
log b ( x y ) = y ∙ log b ( x )
Například:
log 10 (2 8 ) = 8 ∙ log 10 (2)
Logaritmické pravidlo základního přepínání
Základní b logaritmus c je 1 děleno základním c logaritmem b.
log b ( c ) = 1 / log c ( b )
Například:
log 2 (8) = 1 / log 8 (2)
Logaritmické základní pravidlo změny
Základní b logaritmus x je základní c logaritmus x dělený základním c logaritmus b.
log b ( x ) = log c ( x ) / log c ( b )
Například pro výpočet log 2 (8) v kalkulačce musíme změnit základnu na 10:
log 2 (8) = log 10 (8) / log 10 (2)
Viz: pravidlo změny základního protokolu
Logaritmus záporného čísla
Základní b reálný logaritmus x, když x <= 0 není definováno, když x je záporné nebo rovno nule:
log b ( x ) není definováno, když x ≤ 0
Logaritmus 0
Nulový základní b logaritmus není definován:
log b (0) není definován
Limita základního b logaritmu x, když se x blíží nule, je minus nekonečno:
![]()
Viz: log nuly
Logaritmus 1
Základní b logaritmus jedné je nula:
log b (1) = 0
Například základ dvou logaritmů jednoho je nula:
log 2 (1) = 0
Viz: protokol jednoho
Logaritmus nekonečna
Limita základního b logaritmu x, když se x blíží nekonečnu, se rovná nekonečnu:
lim log b ( x ) = ∞, když x → ∞
Viz: protokol nekonečna
Logaritmus základny
Základní b logaritmus b je jeden:
log b ( b ) = 1
Například základní dva logaritmy dvou jsou jeden:
log 2 (2) = 1
Logaritmická derivace
Když
f ( x ) = log b ( x )
Potom derivace f (x):
f ' ( x ) = 1 / ( x ln ( b ))
Viz: log derivát
Logaritmus integrální
Integrál logaritmu x:
∫ log b ( x ) dx = x ∙ (log b ( x ) - 1 / ln ( b ) ) + C
Například:
∫ log 2 ( x ) dx = x ∙ (log 2 ( x ) - 1 / ln (2) ) + C
Logaritmická aproximace
log 2 ( x ) ≈ n + ( x / 2 n - 1),
Složitý logaritmus
Pro komplexní číslo z:
z = re iθ = x + iy
Komplexní logaritmus bude (n = ... - 2, -1,0,1,2, ...):
Log z = ln ( r ) + i ( θ + 2nπ ) = ln (√ ( x 2 + y 2 )) + i · arctan ( y / x ))
Logaritmické problémy a odpovědi
Problém č. 1
Najděte x pro
log 2 ( x ) + log 2 ( x -3) = 2
Řešení:
Použití pravidla produktu:
log 2 ( x ∙ ( x -3)) = 2
Změna formy logaritmu podle definice logaritmu:
x ∙ ( x -3) = 2 2
Nebo
x 2 -3 x -4 = 0
Řešení kvadratické rovnice:
x 1,2 = [3 ± √ (9 + 16)] / 2 = [3 ± 5] / 2 = 4, -1
Protože logaritmus není definován pro záporná čísla, odpověď zní:
x = 4
Problém č. 2
Najděte x pro
log 3 ( x +2) - log 3 ( x ) = 2
Řešení:
Použití pravidla kvocientu:
log 3 (( x +2) / x ) = 2
Změna formy logaritmu podle definice logaritmu:
( x +2) / x = 3 2
Nebo
x +2 = 9 x
Nebo
8 x = 2
Nebo
x = 0,25
Graf protokolu (x)
log (x) není definován pro skutečné ne kladné hodnoty x:
Tabulka logaritmů
| x | přihlásit 10 x | přihlásit 2 x | přihlásit e x |
|---|---|---|---|
| 0 | nedefinováno | nedefinováno | nedefinováno |
| 0 + | - ∞ | - ∞ | - ∞ |
| 0,0001 | -4 | -13,287712 | -9,210340 |
| 0,001 | -3 | -9,965784 | -6,907755 |
| 0,01 | -2 | -6,643856 | -4,605170 |
| 0,1 | -1 | -3,321928 | -2,302585 |
| 1 | 0 | 0 | 0 |
| 2 | 0,301030 | 1 | 0,693147 |
| 3 | 0,4777121 | 1,584963 | 1,098612 |
| 4 | 0,602060 | 2 | 1,386294 |
| 5 | 0,698970 | 2.321928 | 1,609438 |
| 6 | 0,778151 | 2,584963 | 1,791759 |
| 7 | 0,845098 | 2,807355 | 1.945910 |
| 8 | 0,903090 | 3 | 2,079442 |
| 9 | 0,954243 | 3,169925 | 2,197225 |
| 10 | 1 | 3,321928 | 2,302585 |
| 20 | 1,301030 | 4,321928 | 2,995732 |
| 30 | 1,477121 | 4,906891 | 3,401197 |
| 40 | 1,602060 | 5,321928 | 3,688879 |
| 50 | 1,698970 | 5,643856 | 3,912023 |
| 60 | 1,778151 | 5,906991 | 4,094345 |
| 70 | 1,845098 | 6.129283 | 4,248495 |
| 80 | 1,903090 | 6,321928 | 4.382027 |
| 90 | 1,954243 | 6,49 1853 | 4,499810 |
| 100 | 2 | 6,643856 | 4,605170 |
| 200 | 2,301030 | 7,643856 | 5,198317 |
| 300 | 2,477121 | 8.228819 | 5,703782 |
| 400 | 2,602060 | 8,643856 | 5,991465 |
| 500 | 2,698970 | 8,965784 | 6,214608 |
| 600 | 2,778151 | 9,28819 | 6,396930 |
| 700 | 2,845098 | 9,451211 | 6,55 1080 |
| 800 | 2,903090 | 9,643856 | 6,684612 |
| 900 | 2,954243 | 9,813781 | 6,802395 |
| 1000 | 3 | 9,965784 | 6,907755 |
| 10 000 | 4 | 13,287712 | 9,210340 |
Viz také
- Logaritmická pravidla
- Logaritmická změna základny
- Logaritmus nuly
- Logaritmus jednoho
- Logaritmus nekonečna
- Logaritmus záporného čísla
- Logaritmická kalkulačka
- Logaritmický graf
- Logaritmická tabulka
- Kalkulačka přirozeného logaritmu
- Přirozený logaritmus - ln x
- e konstantní
- Decibel (dB)
