Forventningsværdi

Efter sandsynlighed og statistik er forventningen eller den forventede værdi den vægtede gennemsnitlige værdi af en tilfældig variabel.

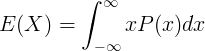
$E (X) = \ int _ {- \ infty} ^ {\ infty} xP (x) dx$

E ( X ) er forventningsværdien af den kontinuerlige tilfældige variabel X

x er værdien af den kontinuerlige tilfældige variabel X

P ( x ) er sandsynlighedsdensitetsfunktionen

$E (X) = \ sum_ {i} ^ {} x_iP (x)$

E ( X ) er forventningsværdien af den kontinuerlige tilfældige variabel X

x er værdien af den kontinuerlige tilfældige variabel X

P ( x ) er sandsynlighedsmassefunktionen for X

Når a er konstant og X, er Y tilfældige variabler:

E ( aX ) = aE ( X )

E ( X + Y ) = E ( X ) + E ( Y )

Når c er konstant:

E ( c ) = c

Når X og Y er uafhængige tilfældige variabler:

E ( X ⋅Y ) = E ( X ) ⋅ E ( Y )

Se også