Variation

I sandsynlighed og statistik er variansen af en tilfældig variabel den gennemsnitlige værdi af kvadratafstanden fra middelværdien. Det repræsenterer, hvordan den tilfældige variabel fordeles nær middelværdien. Lille varians angiver, at den tilfældige variabel er fordelt nær middelværdien. Stor varians angiver, at den tilfældige variabel er fordelt langt fra middelværdien. For eksempel med normalfordeling vil smal klokkekurve have lille varians, og bred klokkekurve vil have stor varians.

Variansdefinition

Variansen af tilfældig variabel X er den forventede værdi af kvadrater med forskellen på X og den forventede værdi μ.

σ ² = Var ( X ) = E [( X - μ ) ² ]

Fra definitionen af den varians, vi kan få

σ ² = Var ( X ) = E ( X ² ) - μ ²

Varians af kontinuerlig tilfældig variabel

For kontinuerlig tilfældig variabel med middelværdien μ og sandsynlighedsdensitetsfunktion f (x):

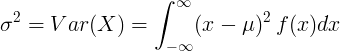
$\ sigma ^ 2 = Var (X) = \ int _ {- \ infty} ^ {\ infty} (x- \ mu) ^ 2 \: f (x) dx$

eller

$Var (X) = \ left [\ int _ {- \ infty} ^ {\ infty} x ^ 2 \: f (x) dx \ right] - \ mu ^ 2$

Varians af diskret tilfældig variabel

For diskret tilfældig variabel X med middelværdien μ og sandsynlighedsmassefunktion P (x):

$\ sigma ^ 2 = Var (X) = \ sum_ {i} ^ {} (x_i- \ mu _X) ^ 2P_X (x_i)$

eller

$Var (X) = \ venstre [\ sum_ {i} ^ {} x_i ^ 2P (x_i) \ højre] - \ mu ^ 2$

Variansegenskaber

Når X og Y er uafhængige tilfældige variabler:

Var ( X + Y ) = Var ( X ) + Var ( Y )

Standardafvigelse ►

Variation

Variansdefinition

Varians af kontinuerlig tilfældig variabel

Varians af diskret tilfældig variabel

Variansegenskaber

Var ( X + Y ) = Var ( X ) + Var ( Y )

Se også

Sandsynlighed og statistik

HUKyLabsIGE TABLER