Standardafvigelse

I sandsynlighed og statistik er standardafvigelsen for en tilfældig variabel den gennemsnitlige afstand for en tilfældig variabel fra middelværdien.

Det repræsenterer, hvordan den tilfældige variabel fordeles nær middelværdien. Lille standardafvigelse indikerer, at den tilfældige variabel er fordelt nær middelværdien. Stor standardafvigelse indikerer, at den tilfældige variabel er fordelt langt fra middelværdien.

Formel for definition af standardafvigelse

Standardafvigelsen er kvadratroden af ​​variansen af ​​tilfældig variabel X med middelværdien μ.

\ sigma = std (X) = \ sqrt {Var (X)} = \ sqrt {E ((X- \ mu) ^ 2}

Fra definitionen af ​​standardafvigelsen kan vi få

\ sigma = std (X) = \ sqrt {E (X ^ 2) - \ mu ^ 2}

Standardafvigelse for kontinuerlig tilfældig variabel

For kontinuerlig tilfældig variabel med middelværdien μ og sandsynlighedsdensitetsfunktion f (x):

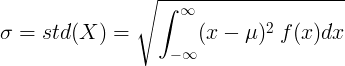
\ sigma = std (X) = \ sqrt {\ int _ {- \ infty} ^ {\ infty} (x- \ mu) ^ 2 \: f (x) dx}

eller

\ sigma = std (X) = \ sqrt {\ left [\ int _ {- \ infty} ^ {\ infty} x ^ 2 \: f (x) dx \ right] - \ mu ^ 2}

Standardafvigelse af diskret tilfældig variabel

For diskret tilfældig variabel X med middelværdien μ og sandsynlighedsmassefunktion P (x):

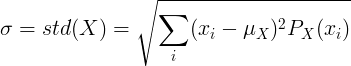
\ sigma = std (X) = \ sqrt {\ sum_ {i} ^ {} (x_i- \ mu _X) ^ 2P_X (x_i)}

eller

\ sigma = std (X) = \ sqrt {\ left [\ sum_ {i} ^ {} x_i ^ 2P (x_i) \ right] - \ mu ^ 2}

 

Sandsynlighedsfordeling ►

 

Se også

Sandsynlighed og statistik
HUKyLabsIGE TABLER