Sandsynlighedsfordeling

I sandsynlighed og statistik er distribution en egenskab ved en tilfældig variabel, beskriver sandsynligheden for den tilfældige variabel i hver værdi.

Hver distribution har en bestemt sandsynlighedsdensitetsfunktion og sandsynlighedsfordelingsfunktion.

Selvom der er et ubestemt antal sandsynlighedsfordelinger, er der flere almindelige distributioner i brug.

Kumulativ fordelingsfunktion

Sandsynlighedsfordelingen er beskrevet af den kumulative fordelingsfunktion F (x),

hvilket er sandsynligheden for, at den tilfældige variabel X får en værdi, der er mindre end eller lig med x:

F ( x ) = P ( X ≤ x )

Kontinuerlig distribution

Den kumulative fordelingsfunktion F (x) beregnes ved integration af sandsynlighedsdensitetsfunktionen f (u) af kontinuerlig tilfældig variabel X.

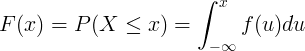
Diskret distribution

Den kumulative fordelingsfunktion F (x) beregnes ved sammenlægning af sandsynlighedsmassefunktionen P (u) for den diskrete tilfældige variabel X.

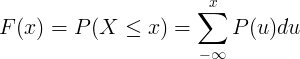
Kontinuerlig distributionstabel

Kontinuerlig fordeling er fordelingen af ​​en kontinuerlig tilfældig variabel.

Eksempel på kontinuerlig distribution

...

Kontinuerlig distributionstabel

Distributionsnavn Distributionssymbol Sandsynlighedsdensitetsfunktion (pdf) Betyde Variation
   

f X ( x )

μ = E ( X )

σ 2 = Var ( X )
Normal / gaussisk

X ~ N (μ, σ 2 )

 \ frac {1} {\ sigma \ sqrt {2 \ pi}} e ^ {- \ frac {(x- \ mu) ^ 2} {2 \ sigma ^ 2}} μ σ 2
Uniform

X ~ U ( a , b )

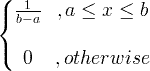 \ begin {Bmatrix} \ frac {1} {ba} &, a \ leq x \ leq b \\ & \\ 0 &, ellers \ end {matrix} \ frac {(ba) ^ 2} {12}
Eksponentiel X ~ exp (λ) \ begin {Bmatrix} \ lambda e ^ {- \ lambda x} & x \ geq 0 \\ 0 & x <0 \ end {matrix} \ frac {1} {\ lambda} \ frac {1} {\ lambda ^ 2}
Gamma X ~ gamma ( c , λ) 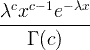\ frac {\ lambda ^ cx ^ {c-1} e ^ {- \ lambda x}} {\ Gamma (c)}

x / 0, c / 0, λ/ 0

 \ frac {c} {\ lambda} \ frac {c} {\ lambda ^ 2}
Chi firkant

X ~ χ 2 ( k )

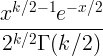 \ frac {x ^ {k / 2-1} e ^ {- x / 2}} {2 ^ {k / 2} \ Gamma (k / 2)}

k

2 k
Wishart        
F

X ~ F ( k 1 , k 2 )

      
Beta        
Weibull        
Log-normal

X ~ LN (μ, σ 2 )

      
Rayleigh        
Cauchy        
Dirichlet        
Laplace        
Afgift        
Ris        
Studentens t        

Diskret distributionstabel

Diskret distribution er fordelingen af ​​en diskret tilfældig variabel.

Eksempel på diskret distribution

...

Diskret distributionstabel

Distributionsnavn Distributionssymbol Sandsynlighedsmassefunktion (pmf) Betyde Variation
    f x ( k ) = P ( X = k )

k = 0,1,2, ...

 E ( x ) Var ( x )
Binomial

X ~ Bin ( n , p )

 \ binom {n} {k} p ^ {k} (1-p) ^ {nk}

np

np (1- p )
Poisson

X ~ Poisson (λ)

λ ≥ 0

λ

λ

Uniform

X ~ U ( a, b )

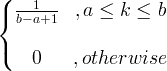 \ begin {Bmatrix} \ frac {1} {b-a + 1} &, a \ leq k \ leq b \\ & \\ 0 &, ellers \ end {matrix} \ frac {a + b} {2} \ frac {(b-a + 1) ^ {2} -1} {12}
Geometrisk

X ~ Geom ( p )

 p (1-p) ^ {k}

\ frac {1-p} {p}

\ frac {1-p} {p ^ 2}
Hypergeometrisk

X ~ HG ( N , K , n )

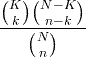N = 0,1,2, ...

K = 0,1, .., N

n = 0,1, ..., N

 \ frac {nK} {N} \ frac {nK (NK) (Nn)} {N ^ 2 (N-1)}
Bernoulli

X ~ Bern ( p )

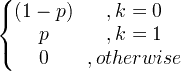 \ begin {Bmatrix} (1-p) &, k = 0 \\ p &, k = 1 \\ 0 &, ellers \ slut {matrix}

p

p (1- p )

 

Se også

Sandsynlighed og statistik
HUKyLabsIGE TABLER