Die Konstante
Die Konstante oder Eulers Zahl ist eine mathematische Konstante. Die e-Konstante ist eine reelle und irrationale Zahl.
e = 2.718281828459 ...
Definition von e
Die e-Konstante ist definiert als die Grenze:
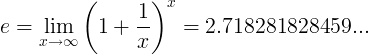
Alternative Definitionen
Die e-Konstante ist definiert als die Grenze:
![]()
Die e-Konstante ist definiert als die unendliche Reihe:
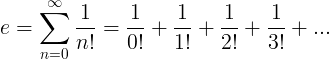
Eigenschaften von e
Kehrwert von e
Der Kehrwert von e ist die Grenze:
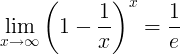
Derivate von e
Die Ableitung der Exponentialfunktion ist die Exponentialfunktion:
( e x ) '= e x
Die Ableitung der natürlichen Logarithmusfunktion ist die reziproke Funktion:
(log e x ) '= (ln x )' = 1 / x
Integrale von e
Das unbestimmte Integral der Exponentialfunktion e x ist die Exponentialfunktion e x .
∫ e x dx = e x + c
Das unbestimmte Integral der natürlichen Logarithmusfunktion log e x ist:
∫ log e x dx = ∫ ln x dx = x ln x - x + c
Das bestimmte Integral von 1 bis e der reziproken Funktion 1 / x ist 1:
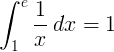
Basis e Logarithmus
Der natürliche Logarithmus einer Zahl x ist definiert als der Basis-e-Logarithmus von x:
ln x = log e x
Exponentialfunktion
Die Exponentialfunktion ist definiert als:
f ( x ) = exp ( x ) = e x
Eulers Formel
Die komplexe Zahl e iθ hat die Identität:
e iθ = cos ( θ ) + i sin ( θ )
i ist die imaginäre Einheit (die Quadratwurzel von -1).
θ ist eine beliebige reelle Zahl.
Siehe auch
- Wie ist e 2.71828183?
- Logarithmusregeln
- Natürlicher Logarithmus
- Exponentenregeln
- Normalverteilung
- Pi-Konstante
- Die Konstante - Wikipedia