Erwartungswert
In Wahrscheinlichkeit und Statistik ist die Erwartung oder der erwartete Wert der gewichtete Durchschnittswert einer Zufallsvariablen.
Erwartung einer kontinuierlichen Zufallsvariablen
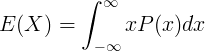
E ( X ) ist der Erwartungswert der kontinuierlichen Zufallsvariablen X.
x ist der Wert der stetigen Zufallsvariablen X.
P ( x ) ist die Wahrscheinlichkeitsdichtefunktion
Erwartung einer diskreten Zufallsvariablen
![]()
E ( X ) ist der Erwartungswert der kontinuierlichen Zufallsvariablen X.
x ist der Wert der stetigen Zufallsvariablen X.
P ( x ) ist die Wahrscheinlichkeitsmassenfunktion von X.
Eigenschaften der Erwartung
Linearität
Wenn a konstant ist und X, Y Zufallsvariablen sind:
E ( aX ) = aE ( X )
E ( X + Y ) = E ( X ) + E ( Y )
Konstante
Wenn c konstant ist:
E ( c ) = c
Produkt
Wenn X und Y unabhängige Zufallsvariablen sind:
E ( X ≤ Y ) = E ( X ) ≤ E ( Y )
bedingte Erwartung
Siehe auch
Wahrscheinlichkeit und Statistik
- Grundwahrscheinlichkeit
- Erwartung
- Varianz
- Standardabweichung
- Wahrscheinlichkeitsverteilung
- Normalverteilung
- Statistiksymbole
SCHNELLE TABELLEN