Standardabweichung

In Wahrscheinlichkeit und Statistik ist die Standardabweichung einer Zufallsvariablen der durchschnittliche Abstand einer Zufallsvariablen vom Mittelwert.

Es zeigt, wie die Zufallsvariable in der Nähe des Mittelwerts verteilt ist. Eine kleine Standardabweichung zeigt an, dass die Zufallsvariable nahe dem Mittelwert verteilt ist. Eine große Standardabweichung zeigt an, dass die Zufallsvariable weit vom Mittelwert entfernt ist.

Standardabweichungsdefinitionsformel

Die Standardabweichung ist die Quadratwurzel der Varianz der Zufallsvariablen X mit einem Mittelwert von μ.

\ sigma = std (X) = \ sqrt {Var (X)} = \ sqrt {E ((X- \ mu) ^ 2}

Aus der Definition der Standardabweichung können wir erhalten

\ sigma = std (X) = \ sqrt {E (X ^ 2) - \ mu ^ 2}

Standardabweichung der kontinuierlichen Zufallsvariablen

Für kontinuierliche Zufallsvariable mit Mittelwert μ und Wahrscheinlichkeitsdichtefunktion f (x):

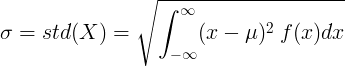
\ sigma = std (X) = \ sqrt {\ int _ {- \ infty} ^ {\ infty} (x- \ mu) ^ 2 \: f (x) dx}

oder

\ sigma = std (X) = \ sqrt {\ left [\ int _ {- \ infty} ^ {\ infty} x ^ 2 \: f (x) dx \ right] - \ mu ^ 2}

Standardabweichung der diskreten Zufallsvariablen

Für diskrete Zufallsvariable X mit Mittelwert μ und Wahrscheinlichkeitsmassenfunktion P (x):

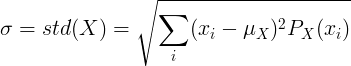
\ sigma = std (X) = \ sqrt {\ sum_ {i} ^ {} (x_i- \ mu _X) ^ 2P_X (x_i)}

oder

\ sigma = std (X) = \ sqrt {\ left [\ sum_ {i} ^ {} x_i ^ 2P (x_i) \ right] - \ mu ^ 2}

 

Wahrscheinlichkeitsverteilung ►

 

Siehe auch

Wahrscheinlichkeit und Statistik
SCHNELLE TABELLEN