Varianz

In Wahrscheinlichkeit und Statistik ist die Varianz einer Zufallsvariablen der Durchschnittswert des quadratischen Abstands vom Mittelwert. Es gibt an, wie die Zufallsvariable in der Nähe des Mittelwerts verteilt ist. Eine kleine Varianz zeigt an, dass die Zufallsvariable nahe dem Mittelwert verteilt ist. Eine große Varianz zeigt an, dass die Zufallsvariable weit vom Mittelwert entfernt ist. Beispielsweise weist bei normaler Verteilung eine schmale Glockenkurve eine geringe Varianz und eine breite Glockenkurve eine große Varianz auf.

Varianzdefinition

Die Varianz der Zufallsvariablen X ist der erwartete Wert der Differenzquadrate von X und der erwartete Wert μ.

σ 2 = Var ( X ) = E [( X - μ ) 2 ]

Aus der Definition der Varianz können wir erhalten

σ 2 = Var ( X ) = E ( X 2 ) - μ 2

Varianz der kontinuierlichen Zufallsvariablen

Für kontinuierliche Zufallsvariable mit Mittelwert μ und Wahrscheinlichkeitsdichtefunktion f (x):

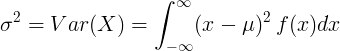
\ sigma ^ 2 = Var (X) = \ int _ {- \ infty} ^ {\ infty} (x- \ mu) ^ 2 \: f (x) dx

oder

Var (X) = \ left [\ int _ {- \ infty} ^ {\ infty} x ^ 2 \: f (x) dx \ right] - \ mu ^ 2

Varianz der diskreten Zufallsvariablen

Für diskrete Zufallsvariable X mit Mittelwert μ und Wahrscheinlichkeitsmassenfunktion P (x):

\ sigma ^ 2 = Var (X) = \ sum_ {i} ^ {} (x_i- \ mu _X) ^ 2P_X (x_i)

oder

Var (X) = \ left [\ sum_ {i} ^ {} x_i ^ 2P (x_i) \ right] - \ mu ^ 2

Eigenschaften der Varianz

Wenn X und Y unabhängige Zufallsvariablen sind:

Var ( X + Y ) = Var ( X ) + Var ( Y )

 

Standardabweichung ►

 

Siehe auch

Wahrscheinlichkeit und Statistik
SCHNELLE TABELLEN