Wahrscheinlichkeitsverteilung

In Wahrscheinlichkeit und Statistik ist die Verteilung ein Merkmal einer Zufallsvariablen, beschreibt die Wahrscheinlichkeit der Zufallsvariablen in jedem Wert.

Jede Verteilung hat eine bestimmte Wahrscheinlichkeitsdichtefunktion und Wahrscheinlichkeitsverteilungsfunktion.

Obwohl es eine unbestimmte Anzahl von Wahrscheinlichkeitsverteilungen gibt, werden mehrere gemeinsame Verteilungen verwendet.

Verteilungsfunktion

Die Wahrscheinlichkeitsverteilung wird durch die kumulative Verteilungsfunktion F (x) beschrieben.

Dies ist die Wahrscheinlichkeit, dass die Zufallsvariable X einen Wert kleiner oder gleich x erhält:

F ( x ) = P ( X ≤ x )

Kontinuierliche Verteilung

Die kumulative Verteilungsfunktion F (x) wird durch Integration der Wahrscheinlichkeitsdichtefunktion f (u) der kontinuierlichen Zufallsvariablen X berechnet.

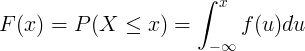
Diskrete Verteilung

Die kumulative Verteilungsfunktion F (x) wird durch Summation der Wahrscheinlichkeitsmassenfunktion P (u) der diskreten Zufallsvariablen X berechnet.

Kontinuierliche Verteilungstabelle

Kontinuierliche Verteilung ist die Verteilung einer kontinuierlichen Zufallsvariablen.

Beispiel für eine kontinuierliche Verteilung

...

Kontinuierliche Verteilungstabelle

Verteilungsname Verteilungssymbol Wahrscheinlichkeitsdichtefunktion (pdf) Bedeuten Varianz
   

f X ( x )

μ = E ( X )

σ 2 = Var ( X )
Normal / Gauß

X ~ N (μ, σ 2 )

 \ frac {1} {\ sigma \ sqrt {2 \ pi}} e ^ {- \ frac {(x- \ mu) ^ 2} {2 \ sigma ^ 2}} μ σ 2
Uniform

X ~ U ( a , b )

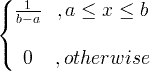 \ begin {Bmatrix} \ frac {1} {ba} &, a \ leq x \ leq b \\ & \\ 0 &, andernfalls \ end {matrix} \ frac {(ba) ^ 2} {12}
Exponentiell X ~ exp (λ) \ begin {Bmatrix} \ lambda e ^ {- \ lambda x} & x \ geq 0 \\ 0 & x <0 \ end {matrix} \ frac {1} {\ lambda} \ frac {1} {\ lambda ^ 2}
Gamma X ~ gamma ( c , λ) 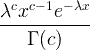\ frac {\ lambda ^ cx ^ {c-1} e ^ {- \ lambda x}} {\ Gamma (c)}

x / 0, c / 0, λ/ 0

 \ frac {c} {\ lambda} \ frac {c} {\ lambda ^ 2}
Chi Quadrat

X ~ χ 2 ( k )

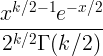 \ frac {x ^ {k / 2-1} e ^ {- x / 2}} {2 ^ {k / 2} \ Gamma (k / 2)}

k

2 k
Wishart        
F

X ~ F ( k 1 , k 2 )

      
Beta        
Weibull        
Log-normal

X ~ LN (μ, σ 2 )

      
Rayleigh        
Cauchy        
Dirichlet        
Laplace        
Erheben        
Reis        
Student's t        

Tabelle der diskreten Verteilungen

Diskrete Verteilung ist die Verteilung einer diskreten Zufallsvariablen.

Beispiel für eine diskrete Verteilung

...

Tabelle der diskreten Verteilungen

Verteilungsname Verteilungssymbol Wahrscheinlichkeitsmassenfunktion (pmf) Bedeuten Varianz
    f x ( k ) = P ( X = k )

k = 0,1,2, ...

 E ( x ) Var ( x )
Binomial

X ~ Bin ( n , p )

 \ binom {n} {k} p ^ {k} (1-p) ^ {nk}

np

np (1- p )
Poisson

X ~ Poisson (λ)

λ ≥ 0

λ

λ

Uniform

X ~ U ( a, b )

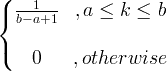 \ begin {Bmatrix} \ frac {1} {b-a + 1} &, a \ leq k \ leq b \\ & \\ 0 &, andernfalls \ end {matrix} \ frac {a + b} {2} \ frac {(b-a + 1) ^ {2} -1} {12}
Geometrisch

X ~ Geom ( p )

 p (1-p) ^ {k}

\ frac {1-p} {p}

\ frac {1-p} {p ^ 2}
Hypergeometrisch

X ~ HG ( N , K , n )

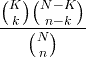N = 0,1,2, ...

K = 0,1, .., N.

n = 0,1, ..., N.

 \ frac {nK} {N} \ frac {nK (NK) (Nn)} {N ^ 2 (N-1)}
Bernoulli

X ~ Bern ( p )

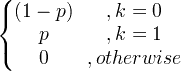 \ begin {Bmatrix} (1-p) &, k = 0 \\ p &, k = 1 \\ 0 &, andernfalls \ end {matrix}

p

p (1- p )

 

Siehe auch

Wahrscheinlichkeit und Statistik
SCHNELLE TABELLEN