Grundlegende Wahrscheinlichkeitsformeln
Wahrscheinlichkeitsbereich
0 ≤ P ( A ) ≤ 1
Regel der ergänzenden Ereignisse
P ( A C ) + P ( A ) = 1
Hinzufügungsregel
P (A∪B) = P (A) + P (B) - P (A∩B)
Disjunkte Ereignisse
Ereignisse A und B sind disjunkt, wenn
P (A∩B) = 0
Bedingte Wahrscheinlichkeit
P (A | B) = P (A∩B) / P (B)
Bayes Formel
P (A | B) = P (B | A) ≤ P (A) / P (B)
Unabhängige Veranstaltungen
Ereignisse A und B sind unabhängig iff
P (A∩B) = P (A) ⋅ P (B)
Verteilungsfunktion
F X ( x ) = P ( X ≤ x )
Wahrscheinlichkeitsmassenfunktion
![]()
Wahrscheinlichkeitsdichtefunktion
![]()
![]()
![]()
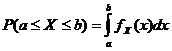
![]()
Kovarianz
![]()
Korrelation
![]()
Bernoulli: 0-Misserfolg 1-Erfolg
Geometrisch: 0-Fehler 1-Erfolg
Hypergeometrisch: N Objekte mit K Erfolgsobjekten, n Objekte werden genommen.
Wahrscheinlichkeit und Statistik
- Grundwahrscheinlichkeit
- Erwartung
- Varianz
- Standardabweichung
- Wahrscheinlichkeitsverteilung
- Normalverteilung
- Statistiksymbole