Αναπόσπαστο

Η ολοκλήρωση είναι η αντίστροφη λειτουργία της παραγωγής.

Το ολοκλήρωμα μιας συνάρτησης είναι η περιοχή κάτω από το γράφημα της συνάρτησης.

Αόριστος ακέραιος ορισμός

Πότε dF (x) / dx = f (x) =/ ακέραιο (f (x) * dx) = F (x) + c

Αόριστες ακέραιες ιδιότητες

ακέραιο (f (x) + g (x)) * dx = ακέραιο (f (x) * dx) + ακέραιο (g (x) * dx)

ακέραιο (a * f (x) * dx) = a * ακέραιο (f (x) * dx)

ακέραιο (f (a * x) * dx) = 1 / a * F (a * x) + c

ακέραιο (f (x + b) * dx) = F (x + b) + c

ακέραιο (f (a * x + b) * dx) = 1 / a * F (a * x + b) + c

ακέραιο (df (x) / dx * dx) = f (x)

Μεταβολή μεταβλητής ολοκλήρωσης

Πότεx = g (τ) καιdx = g '(t) * dt

ακέραιο (f (x) * dx) = ακέραιο (f (g (t)) * g '(t) * dt)

Ενσωμάτωση με ανταλλακτικά

ακέραιο (f (x) * g '(x) * dx) = f (x) * g (x) - ακέραιο (f' (x) * g (x) * dx)

Πίνακας ολοκληρωμένων

ακέραιο (f (x) * dx = F (x) + c

ακέραιο (a * dx) = a * x + c

ακέραιο (x ^ n * dx) = 1 / (a ​​+ 1) * x ^ (a + 1) + c, όταν </ - 1

ακέραιο (1 / x * dx) = ln (abs (x)) + c

ακέραιο (e ^ x * dx) = e ^ x + c

ακέραιο (a ^ x * dx) = a ^ x / ln (x) + c

ακέραιο (ln (x) * dx) = x * ln (x) - x + c

ακέραιο (sin (x) * dx) = -cos (x) + c

ακέραιο (cos (x) * dx) = sin (x) + c

ακέραιο (μαύρισμα (x) * dx) = -ln (abs (cos (x))) + c

ακέραιο (arcsin (x) * dx) = x * arcsin (x) + sqrt (1-x ^ 2) + c

ακέραιο (arccos (x) * dx) = x * arccos (x) - sqrt (1-x ^ 2) + c

ακέραιο (arctan (x) * dx) = x * arctan (x) - 1/2 * ln (1 + x ^ 2) + c

ακέραιο (dx / (ax + b)) = 1 / a * ln (abs (a * x + b)) + c

ακέραιο (1 / sqrt (a ^ 2-x ^ 2) * dx) = arcsin (x / a) + c

ακέραιο (1 / sqrt (x ^ 2 + - a ^ 2) * dx) = ln (abs (x + sqrt (x ^ 2 + - a ^ 2)) + c

ακέραιο (x * sqrt (x ^ 2-a ^ 2) * dx) = 1 / (a ​​* arccos (x / a)) + c

ακέραιο (1 / (a ​​^ 2 + x ^ 2) * dx) = 1 / a * arctan (x / a) + c

ακέραιο (1 / (a ​​^ 2-x ^ 2) * dx) = 1 / 2a * ln (abs (((a + x) / (ax))) + c

ακέραιο (sinh (x) * dx) = cosh (x) + c

ακέραιο (cosh (x) * dx) = sinh (x) + c

ακέραιο (tanh (x) * dx) = ln (cosh (x)) + c

 

Ορισμένος ακέραιος ορισμός

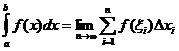
ακέραιο (a..b, f (x) * dx) = lim (n-/ inf, άθροισμα (i = 1..n, f (z (i)) * dx (i))) 

Πότεx0 = a, xn = b

dx (k) = x (k) - x (k-1)

x (k-1) <= z (k) <= x (k)

Ορισμένος ακέραιος υπολογισμός

Πότε ,

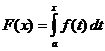 dF (x) / dx = f (x) και

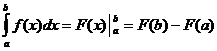
ακέραιο (a..b, f (x) * dx) = F (b) - F (a) 

Ορισμένες ακέραιες ιδιότητες

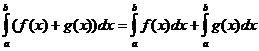
ακέραιο (a..b, (f (x) + g (x)) * dx) = ακέραιο (a..b, f (x) * dx) + ακέραιο (a..b, g (x) * dx )

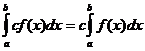
ακέραιο (a..b, c * f (x) * dx) = c * ακέραιο (a..b, f (x) * dx)

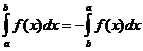
ακέραιο (a..b, f (x) * dx) = - ακέραιο (b..a, f (x) * dx)

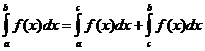
ακέραιο (a..b, f (x) * dx) = integral (a..c, f (x) * dx) + integral (c..b, f (x) * dx)

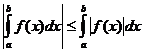
abs (ακέραιο (a..b, f (x) * dx)) <= ακέραιο (a..b, abs (f (x)) * dx)

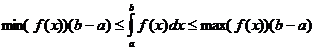min (f (x)) * (ba) <= ακέραιο (a..b, f (x) * dx) <= max (f (x)) * (ba) πότεx μέλος του [a, b]

Μεταβολή μεταβλητής ολοκλήρωσης

Πότεx = g (τ) ,dx = g '(t) * dt ,g (άλφα) = α ,g (beta) = β

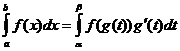
ακέραιο (a..b, f (x) * dx) = ακέραιο (alpha..beta, f (g (t)) * g '(t) * dt)

Ενσωμάτωση με ανταλλακτικά

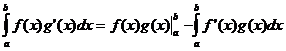
ακέραιο (a..b, f (x) * g '(x) * dx) = integral (a..b, f (x) * g (x) * dx) - ακέραιο (x) * g (x) * dx)

Θεώρημα μέσης τιμής

Όταν το f ( x ) είναι συνεχές υπάρχει ένα σημείογ είναι μέλος του [a, b] Έτσι

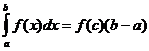
ακέραιο (a..b, f (x) * dx) = f (c) * (ba)  

Τραπεζοειδής προσέγγιση του ορισμένου ακέραιου

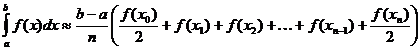
ακέραιο (a..b, f (x) * dx) ~ (ba) / n * (f (x (0)) / 2 + f (x (1)) + f (x (2)) + .. . + f (x (n-1)) + f (x (n)) / 2)

Η συνάρτηση γάμμα

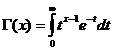
gamma (x) = ολοκλήρωση (0..inf, t ^ (x-1) * e ^ (- t) * dt

Η συνάρτηση Gamma είναι συγκλίνουσα για x/ 0 .

Ιδιότητες λειτουργίας γάμμα

G ( x +1) = x G ( x )

G ( n +1) = n ! , όταν n ℕ (θετικός ακέραιος).είναι μέλος του

Η συνάρτηση Beta

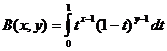
B (x, y) = ακέραιο (0..1, t ^ (n-1) * (1-t) ^ (y-1) * dt

Συναρτήσεις Beta και Gamma Function

B (x, y) = Gamma (x) * Gamma (y) / Gamma (x + y)

 

 

 

ΛΟΓΙΣΜΟΣ
ΓΡΗΓΟΡΑ ΠΙΝΑΚΕΣ