Διαφορά

Στην πιθανότητα και στα στατιστικά στοιχεία, η διακύμανση μιας τυχαίας μεταβλητής είναι η μέση τιμή της τετραγωνικής απόστασης από τη μέση τιμή. Αντιπροσωπεύει τον τρόπο κατανομής της τυχαίας μεταβλητής κοντά στη μέση τιμή. Η μικρή διακύμανση δείχνει ότι η τυχαία μεταβλητή κατανέμεται κοντά στη μέση τιμή. Η μεγάλη διακύμανση δείχνει ότι η τυχαία μεταβλητή κατανέμεται πολύ μακριά από τη μέση τιμή. Για παράδειγμα, με κανονική κατανομή, η στενή καμπύλη καμπάνας θα έχει μικρή διακύμανση και η μεγάλη καμπύλη καμπάνας θα έχει μεγάλη διακύμανση.

Ορισμός διακύμανσης

Η διακύμανση της τυχαίας μεταβλητής X είναι η αναμενόμενη τιμή των τετραγώνων διαφοράς του X και της αναμενόμενης τιμής μ.

σ 2 = Var ( X ) = E [( X - μ ) 2 ]

Από τον ορισμό της διακύμανσης μπορούμε να πάρουμε

σ 2 = Var ( X ) = E ( X 2 ) - μ 2

Διακύμανση συνεχούς τυχαίας μεταβλητής

Για συνεχή τυχαία μεταβλητή με μέση τιμή μ και συνάρτηση πυκνότητας πιθανότητας f (x):

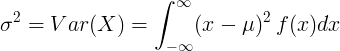
\ sigma ^ 2 = Var (X) = \ int _ {- \ infty} ^ {\ infty} (x- \ mu) ^ 2 \: f (x) dx

ή

Var (X) = \ αριστερά [\ int _ {- \ infty} ^ {\ infty} x ^ 2 \: f (x) dx \ δεξιά] - \ mu ^ 2

Διακύμανση διακριτής τυχαίας μεταβλητής

Για διακριτή τυχαία μεταβλητή X με μέση τιμή μ και συνάρτηση μάζας πιθανότητας P (x):

\ sigma ^ 2 = Var (X) = \ sum_ {i} ^ {} (x_i- \ mu _X) ^ 2P_X (x_i)

ή

Var (X) = \ αριστερά [\ sum_ {i} ^ {} x_i ^ 2P (x_i) \ δεξιά] - \ mu ^ 2

Ιδιότητες διακύμανσης

Όταν τα Χ και Υ είναι ανεξάρτητες τυχαίες μεταβλητές:

Var ( X + Y ) = Var ( X ) + Var ( Y )

 

Τυπική απόκλιση ►

 

Δείτε επίσης

ΠΙΘΑΝΟΤΗΤΑ & ΣΤΑΤΙΣΤΙΚΕΣ
ΓΡΗΓΟΡΑ ΠΙΝΑΚΕΣ