Κατανομή πιθανότητας

Στην πιθανότητα και τη στατιστική κατανομή είναι ένα χαρακτηριστικό μιας τυχαίας μεταβλητής, περιγράφει την πιθανότητα της τυχαίας μεταβλητής σε κάθε τιμή.

Κάθε κατανομή έχει μια συγκεκριμένη συνάρτηση πυκνότητας πιθανότητας και συνάρτηση κατανομής πιθανότητας.

Αν και υπάρχει αόριστος αριθμός κατανομών πιθανότητας, υπάρχουν πολλές κοινές κατανομές που χρησιμοποιούνται.

Λειτουργία αθροιστικής διανομής

Η κατανομή πιθανότητας περιγράφεται από τη συνάρτηση αθροιστικής κατανομής F (x),

που είναι η πιθανότητα της τυχαίας μεταβλητής X να πάρει τιμή μικρότερη ή ίση με x:

F ( x ) = P ( X ≤ x )

Συνεχής διανομή

Η συνάρτηση αθροιστικής κατανομής F (x) υπολογίζεται με ενσωμάτωση της συνάρτησης πυκνότητας πιθανότητας f (u) της συνεχούς τυχαίας μεταβλητής X.

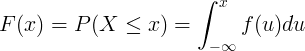
Διακριτή διανομή

Η συνάρτηση αθροιστικής κατανομής F (x) υπολογίζεται με άθροισμα της συνάρτησης πιθανότητας μάζας P (u) διακριτής τυχαίας μεταβλητής X.

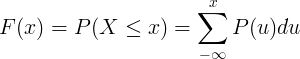
Πίνακας συνεχών διανομών

Η συνεχής κατανομή είναι η κατανομή μιας συνεχούς τυχαίας μεταβλητής.

Παράδειγμα συνεχούς διανομής

...

Πίνακας συνεχών διανομών

Όνομα διανομής Σύμβολο διανομής Συνάρτηση πυκνότητας πιθανότητας (pdf) Σημαίνω Διαφορά
   

f X ( x )

μ = Ε ( X )

σ 2 = Var ( X )
Κανονική / γκάους

X ~ N (μ, σ 2 )

 \ frac {1} {\ sigma \ sqrt {2 \ pi}} e ^ {- \ frac {(x- \ mu) ^ 2} {2 \ sigma ^ 2}} μ σ 2
Στολή

X ~ U ( α , β )

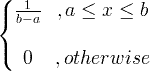 \ begin {Bmatrix} \ frac {1} {ba} &, a \ leq x \ leq b \\ & \\ 0 &, διαφορετικά \ end {matrix} \ frac {(ba) ^ 2} {12}
Εκθετικός X ~ exp (λ) \ start {Bmatrix} \ lambda e ^ {- \ lambda x} & x \ geq 0 \\ 0 & x <0 \ end {matrix} \ frac {1} {\ λάμδα} \ frac {1} {\ lambda ^ 2}
Γάμμα X ~ γάμμα ( c , λ) 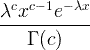\ frac {\ lambda ^ cx ^ {c-1} e ^ {- \ lambda x}} {\ Γάμμα (γ)}

x / 0, c / 0, λ/ 0

 \ frac {c} {\ λάμδα} \ frac {c} {\ lambda ^ 2}
Πλατεία Τσι

X ~ χ 2 ( k )

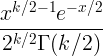 \ frac {x ^ {k / 2-1} e ^ {- x / 2}} {2 ^ {k / 2} \ Gamma (k / 2)}

κ

2 κ
Ουίσαρτ        
ΣΤ

X ~ F ( k 1 , k 2 )

      
Βήτα        
Weibull        
Συνήθης καταγραφή

X ~ LN (μ, σ 2 )

      
Ρέιλι        
Cauchy        
Ντίριχλετ        
Laplace        
Είσπραξη        
Ρύζι        
Μαθητής τ        

Πίνακας διακριτών διανομών

Η διακριτή κατανομή είναι η κατανομή μιας διακριτής τυχαίας μεταβλητής.

Παράδειγμα διακριτής διανομής

...

Πίνακας διακριτών διανομών

Όνομα διανομής Σύμβολο διανομής Συνάρτηση μάζας πιθανότητας (pmf) Σημαίνω Διαφορά
    f x ( k ) = P ( X = k )

k = 0,1,2, ...

 Ε ( x ) Var ( x )
Διωνυμικός

X ~ Κάδος ( n , p )

 \ binom {n} {k} p ^ {k} (1-p) ^ {nk}

np

np (1- p )
Poisson

X ~ Poisson (λ)

λ ≥ 0

λ

λ

Στολή

X ~ U ( α, β )

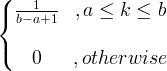 \ begin {Bmatrix} \ frac {1} {b-a + 1} &, a \ leq k \ leq b \\ & \\ 0 &, διαφορετικά \ end {matrix} \ frac {a + b} {2} \ frac {(b-a + 1) ^ {2} -1} {12}
Γεωμετρικός

X ~ Geom ( σελ )

 p (1-p) ^ {k}

\ frac {1-p} {p}

\ frac {1-p} {p ^ 2}
Υπερ-γεωμετρικά

X ~ HG ( N , K , n )

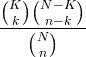Ν = 0,1,2, ...

Κ = 0,1, .., Ν

n = 0,1, ..., Ν

 \ frac {nK} {N} \ frac {nK (NK) (Nn)} {N ^ 2 (N-1)}
Μπερνούλι

Χ ~ Βέρνη ( σελ )

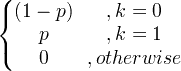 \ begin {Bmatrix} (1-p) &, k = 0 \\ p &, k = 1 \\ 0 &, διαφορετικά \ end {matrix}

σελ.

p (1- p )

 

Δείτε επίσης

ΠΙΘΑΝΟΤΗΤΑ & ΣΤΑΤΙΣΤΙΚΕΣ
ΓΡΗΓΟΡΑ ΠΙΝΑΚΕΣ