Βασικοί τύποι πιθανότητας
Εύρος πιθανότητας
0 ≤ P ( A ) ≤ 1
Κανόνας συμπληρωματικών εκδηλώσεων
P ( A C ) + P ( A ) = 1
Κανόνας προσθήκης
P (A∪B) = P (A) + P (B) - P (A∩B)
Διακοπή εκδηλώσεων
Τα συμβάντα Α και Β είναι χωριστά
P (A∩B) = 0
Πιθανότητα υπό όρους
P (A | B) = P (A∩B) / P (B)
Φόρμουλα Bayes
P (A | B) = P (B | A) ⋅ P (A) / P (B)
Ανεξάρτητες εκδηλώσεις
Οι εκδηλώσεις Α και Β είναι ανεξάρτητες
P (A∩B) = P (A) ⋅ P (B)
Λειτουργία αθροιστικής κατανομής
F X ( x ) = P ( X ≤ x )
Συνάρτηση μάζας πιθανότητας
![]()
Συνάρτηση πυκνότητας πιθανότητας
![]()
![]()
![]()
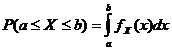
![]()
Συνδιακύμανση
![]()
Συσχέτιση
![]()
Bernoulli: 0-αποτυχία 1-επιτυχία
Γεωμετρική: 0-αποτυχία 1-επιτυχία
Υπεργεωμετρική: N αντικείμενα με K επιτυχία αντικείμενα, n αντικείμενα λαμβάνονται.
ΠΙΘΑΝΟΤΗΤΑ & ΣΤΑΤΙΣΤΙΚΕΣ
- Βασική πιθανότητα
- Προσδοκία
- Διαφορά
- Τυπική απόκλιση
- Κατανομή πιθανότητας
- Κανονική κατανομή
- Στατιστικά σύμβολα