Συνάρτηση Arccos (x)
Arccos (x), cos -1 (x), αντίστροφη συνωστίνη .
Ορισμός Arccos
Το συνημίτονο τόξου χ ορίζεται ως το αντίστροφο συνημίτονο συνάρτηση του x όταν -1≤x≤1.
Όταν το συνημίτονο του y είναι ίσο με x:
cos y = x
Στη συνέχεια, η αρκοσίνη του x είναι ίση με την αντίστροφη συνωστίνη του x, η οποία είναι ίση με y:
arccos x = cos -1 x = y
(Εδώ cos -1 x σημαίνει το αντίστροφο συνημίτονο και δεν σημαίνει συνημίτονο με την ισχύ του -1).
Παράδειγμα
arccos 1 = cos -1 1 = 0 rad = 0 °
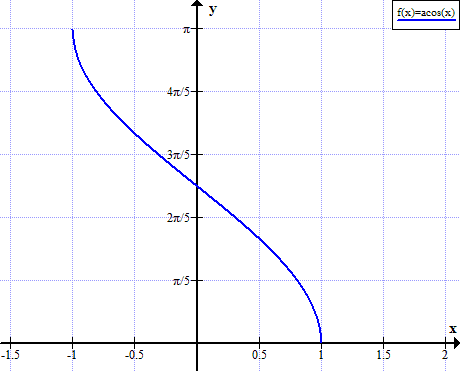
Γράφημα των arccos
Κανόνες Arccos
| Όνομα κανόνα | Κανόνας |
|---|---|
| Συνημίτονο της αρκοσίνης | cos (arccos x ) = x |
| Αρκοσίνη συνημίτονο | arccos (cos x ) = x + 2 k π, όταν k ∈ℤ ( k είναι ακέραιος) |
| Arccos του αρνητικού επιχειρήματος | arccos (- x ) = π - arccos x = 180 ° - arccos x |
| Συμπληρωματικές γωνίες | arccos x = π / 2 - τόξο x = 90 ° - τόξο x |
| Άθροισμα Arccos | arccos ( α ) + arccos ( β ) = arccos ( αβ - √ (1- α 2 ) (1- β 2 ) ) |
| Διαφορά Arccos | arccos ( α ) - arccos ( β ) = arccos ( αβ + √ (1- α 2 ) (1- β 2 ) ) |
| Arccos της αμαρτίας του x | arccos (sin x ) = - x - (2 k +0,5) π |
| Ημιτονοειδής αρκοσίνη | |
| Εφαπτομένη αρκοσίνης | 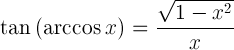 |
| Παράγωγο της αρκοσίνης | 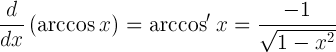 |
| Αόριστη ολοκλήρωση της αρκοσίνης | |
Τραπέζι Arccos
| x | τόξα (x) (ραδ) |
τόξα (x) (°) |
|---|---|---|
| -1 | π | 180 ° |
| -√ 3 /2 | 5π / 6 | 150 ° |
| -√ 2 /2 | 3π / 4 | 135 ° |
| -1/2 | 2π / 3 | 120 ° |
| 0 | π / 2 | 90 ° |
| 1/2 | π / 3 | 60 ° |
| √ 2 /2 | π / 4 | 45 ° |
| √ 3 /2 | π / 6 | 30 ° |
| 1 | 0 | 0 ° |
Δείτε επίσης
- Λειτουργία συνημίτονου
- Λειτουργία Arcsine
- Αρκτική λειτουργία
- Αριθμομηχανή Arccos
- Μετατροπέας ακτίνων σε βαθμούς
- Arccos του 0
- Arccos του 1
- Arccos από 2
- Arccos του 3
- Arccos του cos
- Arccos της αμαρτίας
- Παράγωγο Arccos
- Γράφημα Arccos
- Μαρούλι arccos
- Αμαρτία arccos
- Μαυρίκι από arccos