Ootusväärtus
Tõenäosuses ja statistikas on ootus või eeldatav väärtus juhusliku suuruse kaalutud keskmine väärtus.
Pideva juhusliku muutuja ootus
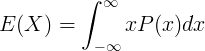
E ( X ) on pideva juhusliku muutuja X eeldatav väärtus
x on pideva juhusliku muutuja X väärtus
P ( x ) on tõenäosustiheduse funktsioon
Diskreetse juhusliku muutuja ootus
![]()
E ( X ) on pideva juhusliku muutuja X eeldatav väärtus
x on pideva juhusliku muutuja X väärtus
P ( x ) on X tõenäosusmassi funktsioon
Ootuse omadused
Lineaarsus
Kui a on konstant ja X, Y on juhuslikud muutujad:
E ( aX ) = aE ( X )
E ( X + Y ) = E ( X ) + E ( Y )
Pidev
Kui c on konstantne:
E ( c ) = c
Toode
Kui X ja Y on sõltumatud juhuslikud muutujad:
E ( X ⋅ Y ) = E ( X ) ⋅ E ( Y )
tingimuslik ootus
Vaata ka
TÕENÄOSUS JA STATISTIKA
- Põhitõenäosus
- Ootus
- Dispersioon
- Standardhälve
- Tõenäosuse jaotus
- Normaalne jaotus
- Statistika sümbolid
KIIRED TABELID