Tõenäosuse jaotus
Tõenäosuses ja statistikas on jaotus juhusliku suuruse tunnus, kirjeldab juhusliku muutuja tõenäosust igas väärtuses.
Igal jaotusel on kindel tõenäosustiheduse ja tõenäosusejaotuse funktsioon.
Ehkki tõenäosusjaotusi on määramata arv, on kasutusel mitu levinud jaotust.
Kumulatiivse jaotuse funktsioon
Tõenäosuse jaotust kirjeldatakse kumulatiivse jaotuse funktsiooniga F (x),
mis on juhusliku muutuja X tõenäosus saada väärtus, mis on väiksem või võrdne x:
F ( x ) = P ( X ≤ x )
Pidev levitamine
Kumulatiivse jaotuse funktsioon F (x) arvutatakse pideva juhusliku muutuja X tõenäosustiheduse funktsiooni f (u) integreerimise teel.
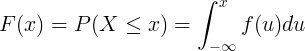
Diskreetne jaotus
Kumulatiivne jaotusfunktsioon F (x) arvutatakse diskreetse juhusliku suuruse X tõenäosusmassifunktsiooni P (u) liitmise teel.
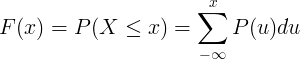
Pidevate jaotuste tabel
Pidev jaotus on pideva juhusliku muutuja jaotumine.
Pideva jaotuse näide
...
Pidevate jaotuste tabel
| Levitamise nimi | Levitamise sümbol | Tõenäosustiheduse funktsioon (pdf) | Tähendab | Dispersioon |
|---|---|---|---|---|
| f X ( x ) |
μ = E ( X ) |
σ 2 = var ( X ) |
||
| Normaalne / gaussian | X ~ N (μ, σ 2 ) |
|
μ | σ 2 |
| Ühtlane | X ~ U ( a , b ) |
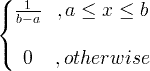 |
|
|
| Eksponentsiaalne | X ~ exp (λ) | |
|
|
| Gamma | X ~ gamma ( c , λ) | 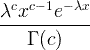 x / 0, c / 0, λ/ 0 |
|
|
| Chi väljak | X ~ χ 2 ( k ) |
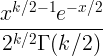 |
k |
2 k |
| Wishart | ||||
| F | X ~ F ( k 1 , k 2 ) |
|||
| Beeta | ||||
| Weibull | ||||
| Logi normaalne | X ~ LN (μ, σ 2 ) |
|||
| Rayleigh | ||||
| Cauchy | ||||
| Dirichlet | ||||
| Laplace | ||||
| Levy | ||||
| Riis | ||||
| Üliõpilase t |
Diskreetsete jaotuste tabel
Diskreetne jaotus on diskreetse juhusliku suuruse jaotus.
Diskreetse jaotuse näide
...
Diskreetsete jaotuste tabel
| Levitamise nimi | Levitamise sümbol | Tõenäosuse massifunktsioon (pmf) | Tähendab | Dispersioon | |
|---|---|---|---|---|---|
| f x ( k ) = P ( X = k ) k = 0,1,2, ... |
E ( x ) | Var ( x ) | |||
| Binomiaalne | X ~ prügikast ( n , p ) |
|
np |
np (1- p ) |
|
| Poisson | X ~ Poisson (λ) |
|
λ ≥ 0 |
λ |
λ |
| Ühtlane | X ~ U ( a, b ) |
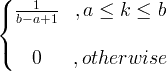 |
|
|
|
| Geomeetriline | X ~ Geom ( p ) |
|
|
|
|
| Hüpergeomeetriline | X ~ HG ( N , K , n ) |
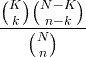 |
N = 0,1,2, ... K = 0,1, .., N n = 0,1, ..., N |
|
|
| Bernoulli | X ~ Bern ( p ) |
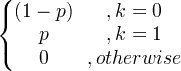 |
p |
p (1- p ) |
|
Vaata ka
TÕENÄOSUS JA STATISTIKA
- Põhitõenäosus
- Ootus
- Dispersioon
- Standardhälve
- Tõenäosuse jaotus
- Normaalne jaotus
- Statistika sümbolid
KIIRED TABELID