Dispersioon

Tõenäosuses ja statistikas on juhusliku suuruse dispersioon ruudukauguse keskmine väärtus keskmisest väärtusest. See tähistab juhusliku muutuja jaotumist keskmise väärtuse lähedal. Väike dispersioon näitab, et juhuslik muutuja jaotub keskmise väärtuse lähedal. Suur dispersioon näitab, et juhuslik muutuja on jaotatud keskmisest väärtusest kaugel. Näiteks normaalse jaotuse korral on kitsal kellakõveral väike dispersioon ja laia kellakõvera dispersioon suur.

Dispersiooni määratlus

Juhusliku suuruse X dispersioon on X erinevuse ruutude eeldatav väärtus ja eeldatav väärtus μ.

σ 2 = Var ( X ) = E [( X - μ ) 2 ]

Dispersiooni määratlusest saame

σ 2 = Var ( X ) = E ( X 2 ) - μ 2

Pideva juhusliku muutuja variatsioon

Pideva juhusliku suuruse korral keskmise väärtusega μ ja tõenäosustiheduse funktsiooniga f (x):

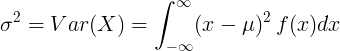
\ sigma ^ 2 = Var (X) = \ int _ {- \ infty} ^ {\ infty} (x- \ mu) ^ 2 \: f (x) dx

või

Var (X) = \ vasak [\ int _ {- \ infty} ^ {\ infty} x ^ 2 \: f (x) dx \ right] - \ mu ^ 2

Diskreetse juhusliku suuruse dispersioon

Diskreetse juhusliku suuruse X korral, mille keskmine väärtus on μ ja tõenäosusmassfunktsioon P (x):

\ sigma ^ 2 = Var (X) = \ summa_ {i} ^ {} (x_i- \ mu _X) ^ 2P_X (x_i)

või

Var (X) = \ vasak [\ summa_ {i} ^ {} x_i ^ 2P (x_i) \ parem] - \ mu ^ 2

Dispersiooni omadused

Kui X ja Y on sõltumatud juhuslikud muutujad:

Var ( X + Y ) = Var ( X ) + Var ( Y )

 

Standardhälve ►

 

Vaata ka

TÕENÄOSUS JA STATISTIKA
KIIRED TABELID