Standardhälve

Tõenäosuses ja statistikas on juhusliku suuruse standardhälve juhusliku suuruse keskmine kaugus keskmisest väärtusest.

See näitab, kuidas juhuslik muutuja jaotub keskmise väärtuse lähedal. Väike standardhälve näitab, et juhuslik muutuja jaotub keskmise väärtuse lähedal. Suur standardhälve näitab, et juhuslik muutuja on hajutatud keskmisest väärtusest kaugel.

Standardhälbe määratluse valem

Standardhälve on juhusliku suuruse X dispersiooni ruutjuur keskmise väärtusega μ.

\ sigma = std (X) = \ sqrt {Var (X)} = \ sqrt {E ((X- \ mu) ^ 2}

Standardhälbe määratlusest saame

\ sigma = std (X) = \ sqrt {E (X ^ 2) - \ mu ^ 2}

Pideva juhusliku muutuja standardhälve

Pideva juhusliku suuruse korral keskmise väärtusega μ ja tõenäosustiheduse funktsiooniga f (x):

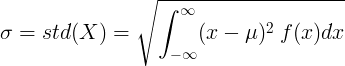
\ sigma = std (X) = \ sqrt {\ int _ {- \ infty} ^ {\ infty} (x- \ mu) ^ 2 \: f (x) dx}

või

\ sigma = std (X) = \ sqrt {\ left [\ int _ {- \ infty} ^ {\ infty} x ^ 2 \: f (x) dx \ right] - \ mu ^ 2}

Diskreetse juhusliku muutuja standardhälve

Diskreetse juhusliku suuruse X korral, mille keskmine väärtus on μ ja tõenäosusmassfunktsioon P (x):

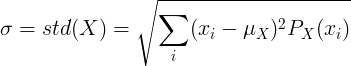
\ sigma = std (X) = \ sqrt {\ sum_ {i} ^ {} (x_i- \ mu _X) ^ 2P_X (x_i)}

või

\ sigma = std (X) = \ sqrt {\ vasakule [\ summa_ {i} ^ {} x_i ^ 2P (x_i) \ paremale] - \ mu ^ 2}

 

Tõenäosuse jaotus ►

 

Vaata ka

TÕENÄOSUS JA STATISTIKA
KIIRED TABELID