Funktsioon Arccos (x)
Arccos (x), cos -1 (x), pöördvõrdeline koosinuse funktsiooni.
Arccose määratlus
Arkuskoosinuse x defineeritakse pöördvõrdeline koosinuse x funktsioonina kui -1≤x≤1.
Kui y koosinus on võrdne x:
cos y = x
Siis on x arkoosiin võrdne x pöördkoosinuse funktsiooniga, mis on võrdne y:
arccos x = cos -1 x = y
(Siin tähendab cos -1 x pöördkoosinust ega tähenda koosinust -1 võimsusele).
Näide
arccos 1 = cos -1 1 = 0 rad = 0 °
Arccose graafik
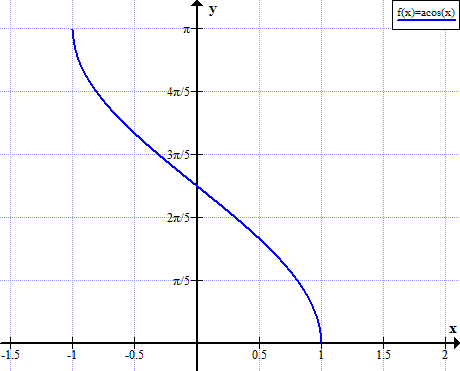
Arccose reeglid
| Reegli nimi | Reegel |
|---|---|
| Arkosiini kosinus | cos (arccos x ) = x |
| Kosinuse arkoosiin | arccos (cos x ) = x + 2 k π, kui k ∈ℤ ( k on täisarv) |
| Negatiivse argumendi arccod | arccos (- x ) = π - arccos x = 180 ° - arccos x |
| Täiendavad nurgad | arccos x = π / 2 - arcsin x = 90 ° - arcsin x |
| Arccose summa | arccos ( α ) + arccos ( β ) = arccos ( αβ - √ (1- α 2 ) (1- β 2 ) ) |
| Arccose erinevus | arccos ( α ) - arccos ( β ) = arccos ( αβ + √ (1- α 2 ) (1- β 2 ) ) |
| X patu arccod | arccos (sin x ) = - x - (2 k +0,5) π |
| Arkoosiini siinus | |
| Arkosiini tangent |  |
| Arkosiini derivaat | 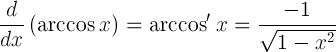 |
| Arkokosiini määramatu integraal | |
Arccose laud
| x | arccos (x) (rad) |
arccos (x) (°) |
|---|---|---|
| -1 | π | 180 ° |
| -√ 3 /2 | 5π / 6 | 150 ° |
| -√ 2 /2 | 3π / 4 | 135 ° |
| -1/2 | 2π / 3 | 120 ° |
| 0 | π / 2 | 90 ° |
| 1/2 | π / 3 | 60 ° |
| √ 2 /2 | π / 4 | 45 ° |
| √ 3 /2 | π / 6 | 30 ° |
| 1 | 0 | 0 ° |
Vaata ka
- Kosinuse funktsioon
- Arcsine funktsioon
- Arktika talitlus
- Arccose kalkulaator
- Radiaanid kraadides muundur
- 0 arccos
- 1 arccos
- Arccos 2-st
- Arccos 3-st
- Arccos of cos
- Arccos pattu
- Arccose derivaat
- Arccose graafik
- Arccose Cos
- Arccose patt
- Arccose tan
TRIGONOMEETRIA
- Arccose funktsioon
- Arcsini funktsioon
- Arktani funktsioon
- Kosinuse funktsioon
- Siinusfunktsioon
- Tangendi funktsioon