Varianssi

Todennäköisyydessä ja tilastossa satunnaismuuttujan varianssi on neliön etäisyyden keskiarvo keskiarvosta. Se edustaa sitä, kuinka satunnaismuuttuja jakautuu lähellä keskiarvoa. Pieni varianssi osoittaa, että satunnaismuuttuja jakautuu lähelle keskiarvoa. Suuri varianssi osoittaa, että satunnaismuuttuja on jaettu kauas keskiarvosta. Esimerkiksi normaalijakaumalla kapealla kellokäyrällä on pieni varianssi ja leveällä kellokäyrällä suuri varianssi.

Varianssin määritelmä

Satunnaismuuttujan X varianssi on X: n erotuskentän ja odotetun arvon μ odotettu arvo.

σ 2 = Var ( X ) = E [( X - μ ) 2 ]

Varianssin määritelmästä voimme saada

σ 2 = Var ( X ) = E ( X 2 ) - μ 2

Jatkuvan satunnaismuuttujan varianssi

Jatkuvalle satunnaismuuttujalle, jonka keskiarvo μ ja todennäköisyystiheysfunktio f (x):

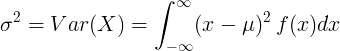
\ sigma ^ 2 = Var (X) = \ int _ {- \ infty} ^ {\ infty} (x- \ mu) ^ 2 \: f (x) dx

tai

Var (X) = \ vasen [\ int _ {- \ infty} ^ {\ infty} x ^ 2 \: f (x) dx \ right] - \ mu ^ 2

Diskreetin satunnaismuuttujan varianssi

Diskreetille satunnaismuuttujalle X, jonka keskiarvo μ ja todennäköisyysmassafunktio P (x):

\ sigma ^ 2 = Var (X) = \ summa_ {i} ^ {} (x_i- \ mu _X) ^ 2P_X (x_i)

tai

Var (X) = \ vasen [\ sum_ {i} ^ {} x_i ^ 2P (x_i) \ oikea] - \ mu ^ 2

Varianssin ominaisuudet

Kun X ja Y ovat riippumattomia satunnaismuuttujia:

Var ( X + Y ) = Var ( X ) + Var ( Y )

 

Keskihajonta ►

 

Katso myös

TODENNAISUUS JA TILASTOT
NOPEAT PÖYTÄT