Todennäköisyysjakauma
Todennäköisyydessä ja tilastoissa jakauma on satunnaismuuttujan ominaisuus, kuvaa satunnaismuuttujan todennäköisyyttä kussakin arvossa.
Jokaisella jakaumalla on tietty todennäköisyystiheysfunktio ja todennäköisyysjakautumisfunktio.
Vaikka todennäköisyysjakaumia on määrittelemätön määrä, käytössä on useita yleisiä jakaumia.
Kumulatiivinen jakaumafunktio
Todennäköisyysjakauma kuvataan kumulatiivisella jakautumisfunktiolla F (x),
mikä on satunnaismuuttujan X todennäköisyys saada arvo, joka on pienempi tai yhtä suuri kuin x:
F ( x ) = P ( X ≤ x )
Jatkuva jakelu
Kumulatiivinen jakautumistoiminto F (x) lasketaan integroimalla jatkuvan satunnaismuuttujan X todennäköisyystiheysfunktio f (u).
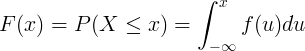
Diskreetti jakauma
Kumulatiivinen jakautumisfunktio F (x) lasketaan diskreetin satunnaismuuttujan X todennäköisyysmassafunktion P (u) summaamalla.
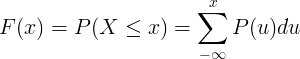
Jatkuvien jakaumien taulukko
Jatkuva jakauma on jatkuvan satunnaismuuttujan jakauma.
Esimerkki jatkuvasta jakelusta
...
Jatkuvien jakaumien taulukko
| Jakelun nimi | Jakelusymboli | Todennäköisyystiheysfunktio (pdf) | Tarkoittaa | Varianssi |
|---|---|---|---|---|
| f X ( x ) |
μ = E ( X ) |
σ 2 = Muuttuja ( X ) |
||
| Normaali / gaussilainen | X ~ N (μ, σ 2 ) |
|
μ | σ 2 |
| Yhtenäinen | X ~ U ( a , b ) |
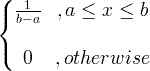 |
|
|
| Eksponentiaalinen | X ~ exp (λ) | |
|
|
| Gamma | X ~ gamma ( c , λ) | 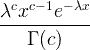 x / 0, c / 0, λ/ 0 |
|
|
| Chi-aukio | X ~ χ 2 ( k ) |
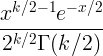 |
k |
2 k |
| Wishart | ||||
| F | X ~ F ( k 1 , k 2 ) |
|||
| Beeta | ||||
| Weibull | ||||
| Loki-normaali | X ~ LN (μ, σ 2 ) |
|||
| Rayleigh | ||||
| Cauchy | ||||
| Dirichlet | ||||
| Laplace | ||||
| Levy | ||||
| Riisi | ||||
| Opiskelijan t |
Diskreetti jakautumataulukko
Diskreetti jakauma on diskreetin satunnaismuuttujan jakauma.
Diskreetti jakaumaesimerkki
...
Diskreetti jakautumataulukko
| Jakelun nimi | Jakelusymboli | Todennäköisyysmassafunktio (pmf) | Tarkoittaa | Varianssi | |
|---|---|---|---|---|---|
| f x ( k ) = P ( X = k ) k = 0,1,2, ... |
E ( x ) | Var ( x ) | |||
| Binomi | X ~ Säiliö ( n , p ) |
|
np |
np (1- p ) |
|
| Poisson | X ~ Poisson (λ) |
|
λ ≥ 0 |
λ |
λ |
| Yhtenäinen | X ~ U ( a, b ) |
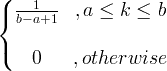 |
|
|
|
| Geometrinen | X ~ Geom ( p ) |
|
|
|
|
| Hypergeometrinen | X ~ HG ( N , K , n ) |
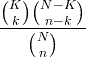 |
N = 0,1,2, ... K = 0,1, .., N n = 0,1, ..., N |
|
|
| Bernoulli | X ~ Bern ( p ) |
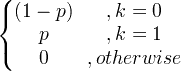 |
p |
p (1- p ) |
|
Katso myös
TODENNAISUUS JA TILASTOT
- Perustodennäköisyys
- Odotus
- Varianssi
- Keskihajonta
- Todennäköisyysjakauma
- Normaalijakauma
- Tilastosymbolit
NOPEAT PÖYTÄT