Todennäköisyyden kaavat

 

Todennäköisyysalue

0 ≤ P ( A ) ≤ 1

Täydentävien tapahtumien sääntö

P ( C ) + P ( ) = 1

Lisäsääntö

P (A∪B) = P (A) + P (B) - P (A∩B)

Disjoint-tapahtumat

Tapahtumat A ja B ovat erimielisiä

P (A∩B) = 0

Ehdollinen todennäköisyys

P (A | B) = P (A∩B) / P (B)

Bayesin kaava

P (A | B) = P (B | A) ⋅ P (A) / P (B)

Riippumattomat tapahtumat

Tapahtumat A ja B ovat itsenäisiä

P (A∩B) = P (A) ⋅ P (B)

Kumulatiivinen jakaumafunktio

F X ( x ) = P ( X ≤ x )

Todennäköisyys massatoiminto

summa (i = 1..n, P (X = x (i)) = 1

Todennäköisyystiheysfunktio

fX (x) = dFX (x) / dx

FX (x) = integraali (-inf..x, fX (y) * dy)

FX (x) = summa (k = 1..x, P (X = k))

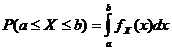
P (a <= X <= b) = integraali (a..b, fX (x) * dx)

integraali (-inf..inf, fX (x) * dx) = 1

 

Kovarianssi

Cox (X, Y) = E (X-ux) (Y-uy) = E (XY) - ux * uy

Korrelaatio

corr (X, Y) = Cov (X, Y) / (Vakio (X) * Vakio (Y))

 

Bernoulli: 0-epäonnistuminen 1-menestys

Geometrinen: 0-epäonnistuminen 1-menestys

Hypergeometrinen: N objektia, joilla on K menestysobjektia, otetaan n objektia.

 

 

 
 
TODENNAISUUS JA TILASTOT
NOPEAT PÖYTÄT