Keskihajonta

Todennäköisyydessä ja tilastossa satunnaismuuttujan keskihajonta on satunnaismuuttujan keskimääräinen etäisyys keskiarvosta.

Se edustaa kuinka satunnaismuuttuja jakautuu lähelle keskiarvoa. Pieni keskihajonta osoittaa, että satunnaismuuttuja jakautuu lähelle keskiarvoa. Suuri keskihajonta osoittaa, että satunnaismuuttuja on jaettu kauas keskiarvosta.

Vakiopoikkeaman määrittelykaava

Keskihajonta on satunnaismuuttujan X varianssin neliöjuuri, keskiarvona μ.

\ sigma = std (X) = \ sqrt {Var (X)} = \ sqrt {E ((X- \ mu) ^ 2}

Vakiopoikkeaman määritelmästä voimme saada

\ sigma = std (X) = \ sqrt {E (X ^ 2) - \ mu ^ 2}

Jatkuvan satunnaismuuttujan keskihajonta

Jatkuvalle satunnaismuuttujalle, jonka keskiarvo μ ja todennäköisyystiheysfunktio f (x):

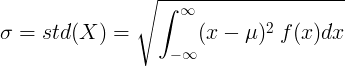
\ sigma = std (X) = \ sqrt {\ int _ {- \ infty} ^ {\ infty} (x- \ mu) ^ 2 \: f (x) dx}

tai

\ sigma = std (X) = \ sqrt {\ vasen [\ int _ {- \ infty} ^ {\ infty} x ^ 2 \: f (x) dx \ right] - \ mu ^ 2}

Diskreetin satunnaismuuttujan keskihajonta

Diskreetille satunnaismuuttujalle X, jonka keskiarvo μ ja todennäköisyysmassafunktio P (x):

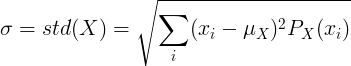
\ sigma = std (X) = \ sqrt {\ sum_ {i} ^ {} (x_i- \ mu _X) ^ 2P_X (x_i)}

tai

\ sigma = std (X) = \ sqrt {\ vasen [\ sum_ {i} ^ {} x_i ^ 2P (x_i) \ oikea] - \ mu ^ 2}

 

Todennäköisyysjakauma ►

 

Katso myös

TODENNAISUUS JA TILASTOT
NOPEAT PÖYTÄT