e constante
La constante ou le nombre d'Euler est une constante mathématique. La constante e est un nombre réel et irrationnel.
e = 2,718281828459 ...
Définition de e
La constante e est définie comme la limite:
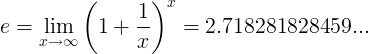
Définitions alternatives
La constante e est définie comme la limite:
![]()
La constante e est définie comme la série infinie:
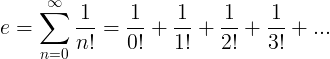
Propriétés de e
Réciproque de e
La réciproque de e est la limite:
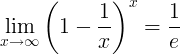
Dérivés de e
La dérivée de la fonction exponentielle est la fonction exponentielle:
( e x ) '= e x
La dérivée de la fonction logarithme naturelle est la fonction réciproque:
(log e x ) '= (ln x )' = 1 / x
Intégrales de e
L'intégrale indéfinie de la fonction exponentielle e x est la fonction exponentielle e x .
∫ e x dx = e x + c
L'intégrale indéfinie de la fonction logarithme népérien log e x est:
∫ log e x dx = ∫ ln x dx = x ln x - x + c
L'intégrale définie de 1 à e de la fonction réciproque 1 / x est 1:
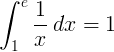
Logarithme de base e
Le logarithme naturel d'un nombre x est défini comme le logarithme de base e de x:
ln x = log e x
Fonction exponentielle
La fonction exponentielle est définie comme:
f ( x ) = exp ( x ) = e x
Formule d'Euler
Le nombre complexe e iθ a l'identité:
e iθ = cos ( θ ) + i sin ( θ )
i est l'unité imaginaire (la racine carrée de -1).
θ est n'importe quel nombre réel.
Voir également
- Comment e est 2,71828183?
- Règles de logarithme
- Un algorithme naturel
- Règles des exposants
- Distribution normale
- Constante Pi
- e constante - wikipedia