Variance
En probabilités et en statistiques, la variance d'une variable aléatoire est la valeur moyenne de la distance carrée par rapport à la valeur moyenne. Il représente la façon dont la variable aléatoire est distribuée près de la valeur moyenne. Une petite variance indique que la variable aléatoire est distribuée près de la valeur moyenne. Une grande variance indique que la variable aléatoire est distribuée loin de la valeur moyenne. Par exemple, avec une distribution normale, une courbe en cloche étroite aura une petite variance et une courbe en cloche large aura une grande variance.
Définition de la variance
La variance de la variable aléatoire X est la valeur attendue des carrés de différence de X et la valeur attendue μ.
σ 2 = Var ( X ) = E [( X - μ ) 2 ]
De la définition de la variance que nous pouvons obtenir
σ 2 = Var ( X ) = E ( X 2 ) - μ 2
Variance de la variable aléatoire continue
Pour une variable aléatoire continue avec valeur moyenne μ et fonction de densité de probabilité f (x):
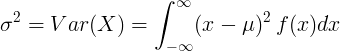
ou
![Var (X) = \ left [\ int _ {- \ infty} ^ {\ infty} x ^ 2 \: f (x) dx \ right] - \ mu ^ 2](variance/cont_var2.gif)
Variance de la variable aléatoire discrète
Pour une variable aléatoire discrète X avec valeur moyenne μ et fonction de masse de probabilité P (x):
![]()
ou
![Var (X) = \ left [\ sum_ {i} ^ {} x_i ^ 2P (x_i) \ right] - \ mu ^ 2](variance/disc_var2.gif)
Propriétés de la variance
Lorsque X et Y sont des variables aléatoires indépendantes:
Var ( X + Y ) = Var ( X ) + Var ( Y )
Voir également
PROBABILITÉ ET STATISTIQUES
- Probabilité de base
- Attente
- Variance
- Écart-type
- Distribution de probabilité
- Distribution normale
- Symboles statistiques
TABLES RAPIDES