Écart-type

En probabilités et en statistiques, l' écart type d'une variable aléatoire est la distance moyenne d'une variable aléatoire par rapport à la valeur moyenne.

Il représente comment la variable aléatoire est distribuée près de la valeur moyenne. Un petit écart type indique que la variable aléatoire est distribuée près de la valeur moyenne. Un grand écart type indique que la variable aléatoire est distribuée loin de la valeur moyenne.

Formule de définition de l'écart type

L'écart type est la racine carrée de la variance de la variable aléatoire X, avec une valeur moyenne de μ.

\ sigma = std (X) = \ sqrt {Var (X)} = \ sqrt {E ((X- \ mu) ^ 2}

De la définition de l'écart type, nous pouvons obtenir

\ sigma = std (X) = \ sqrt {E (X ^ 2) - \ mu ^ 2}

Écart type de la variable aléatoire continue

Pour une variable aléatoire continue avec valeur moyenne μ et fonction de densité de probabilité f (x):

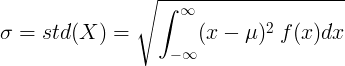
\ sigma = std (X) = \ sqrt {\ int _ {- \ infty} ^ {\ infty} (x- \ mu) ^ 2 \: f (x) dx}

ou

\ sigma = std (X) = \ sqrt {\ left [\ int _ {- \ infty} ^ {\ infty} x ^ 2 \: f (x) dx \ right] - \ mu ^ 2}

Écart type de la variable aléatoire discrète

Pour une variable aléatoire discrète X avec valeur moyenne μ et fonction de masse de probabilité P (x):

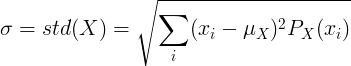
\ sigma = std (X) = \ sqrt {\ sum_ {i} ^ {} (x_i- \ mu _X) ^ 2P_X (x_i)}

ou

\ sigma = std (X) = \ sqrt {\ left [\ sum_ {i} ^ {} x_i ^ 2P (x_i) \ right] - \ mu ^ 2}

 

Distribution de probabilité ►

 

Voir également

PROBABILITÉ ET STATISTIQUES
TABLES RAPIDES