Distribution de probabilité

En probabilité et statistique, la distribution est une caractéristique d'une variable aléatoire, décrit la probabilité de la variable aléatoire dans chaque valeur.

Chaque distribution a une certaine fonction de densité de probabilité et une fonction de distribution de probabilité.

Bien qu'il existe un nombre indéfini de distributions de probabilité, plusieurs distributions courantes sont utilisées.

Fonction de distribution cumulative

La distribution de probabilité est décrite par la fonction de distribution cumulative F (x),

qui est la probabilité de la variable aléatoire X d'obtenir une valeur inférieure ou égale à x:

F ( x ) = P ( X ≤ x )

Distribution continue

La fonction de distribution cumulative F (x) est calculée par intégration de la fonction de densité de probabilité f (u) de la variable aléatoire continue X.

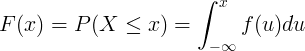
Distribution discrète

La fonction de distribution cumulative F (x) est calculée par sommation de la fonction de masse de probabilité P (u) de la variable aléatoire discrète X.

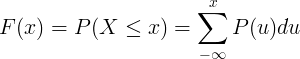
Tableau des distributions continues

La distribution continue est la distribution d'une variable aléatoire continue.

Exemple de distribution continue

...

Tableau des distributions continues

Nom de la distribution Symbole de distribution Fonction de densité de probabilité (pdf) Signifier Variance
   

f X ( x )

μ = E ( X )

σ 2 = Var ( X )
Normal / gaussien

X ~ N (μ, σ 2 )

 \ frac {1} {\ sigma \ sqrt {2 \ pi}} e ^ {- \ frac {(x- \ mu) ^ 2} {2 \ sigma ^ 2}} μ σ 2
Uniforme

X ~ U ( a , b )

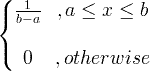 \ begin {Bmatrix} \ frac {1} {ba} &, a \ leq x \ leq b \\ & \\ 0 &, sinon \ end {matrice} \ frac {(ba) ^ 2} {12}
Exponentiel X ~ exp (λ) \ begin {Bmatrix} \ lambda e ^ {- \ lambda x} & x \ geq 0 \\ 0 & x <0 \ end {matrice} \ frac {1} {\ lambda} \ frac {1} {\ lambda ^ 2}
Gamma X ~ gamma ( c , λ) 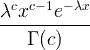\ frac {\ lambda ^ cx ^ {c-1} e ^ {- \ lambda x}} {\ Gamma (c)}

x / 0, c / 0, λ/ 0

 \ frac {c} {\ lambda} \ frac {c} {\ lambda ^ 2}
Chi carré

X ~ χ 2 ( k )

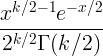 \ frac {x ^ {k / 2-1} e ^ {- x / 2}} {2 ^ {k / 2} \ Gamma (k / 2)}

k

2 km
Wishart        
F

X ~ F ( k 1 , k 2 )

      
Bêta        
Weibull        
Log-normal

X ~ LN (μ, σ 2 )

      
Rayleigh        
Cauchy        
Dirichlet        
Laplace        
Prélèvement        
Riz        
Étudiant t        

Tableau des distributions discrètes

La distribution discrète est la distribution d'une variable aléatoire discrète.

Exemple de distribution discrète

...

Tableau des distributions discrètes

Nom de la distribution Symbole de distribution Fonction de masse de probabilité (pmf) Signifier Variance
    f x ( k ) = P ( X = k )

k = 0,1,2, ...

 E ( x ) Var ( x )
Binôme

X ~ Bin ( n , p )

 \ binom {n} {k} p ^ {k} (1-p) ^ {nk}

np

np (1- p )
Poisson

X ~ Poisson (λ)

λ ≥ 0

λ

λ

Uniforme

X ~ U ( a, b )

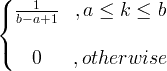 \ begin {Bmatrix} \ frac {1} {b-a + 1} &, a \ leq k \ leq b \\ & \\ 0 &, sinon \ end {matrice} \ frac {a + b} {2} \ frac {(b-a + 1) ^ {2} -1} {12}
Géométrique

X ~ Geom ( p )

 p (1-p) ^ {k}

\ frac {1-p} {p}

\ frac {1-p} {p ^ 2}
Hyper-géométrique

X ~ HG ( N , K , n )

N = 0,1,2, ...

K = 0,1, .., N

n = 0,1, ..., N

 \ frac {nK} {N} \ frac {nK (NK) (Nn)} {N ^ 2 (N-1)}
Bernoulli

X ~ Berne ( p )

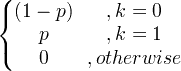 \ begin {Bmatrix} (1-p) &, k = 0 \\ p &, k = 1 \\ 0 &, sinon \ end {matrice}

p

p (1 à p )

 

Voir également

PROBABILITÉ ET STATISTIQUES
TABLES RAPIDES