ચતુર્ભુજ સમીકરણ
ક્વોડ્રેટિક ઇક્વેશન એ બીજા ક્રમનો બહુકોષ છે જેમાં 3 ગુણાંક - એ , બી , સી .
ચતુર્ભુજ સમીકરણ આ દ્વારા આપવામાં આવે છે:
અક્ષ 2 + બીએક્સ + સી = 0
ચતુર્ભુજ સમીકરણનું નિરાકરણ 2 નંબરો x 1 અને x 2 દ્વારા આપવામાં આવે છે .
આપણે ચતુર્ભુજ સમીકરણને આના સ્વરૂપમાં બદલી શકીએ:
( x - x 1 ) ( x - x 2 ) = 0
ચતુર્ભુજ ફોર્મ્યુલા
ચતુર્ભુજ સમીકરણનું નિવારણ ચતુર્ભુજ સૂત્ર દ્વારા આપવામાં આવ્યું છે:
![]()
વર્ગમૂળ અંદર અભિવ્યક્તિ કહેવામાં આવે છે વિવેચન અને Δ દ્વારા સૂચિત કરવામાં આવે છે:
Δ = બી 2 - 4 એસી
ભેદભાવપૂર્ણ સંકેત સાથે ચતુર્ભુજ સૂત્ર:
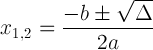
આ અભિવ્યક્તિ મહત્વપૂર્ણ છે કારણ કે તે અમને સોલ્યુશન વિશે કહી શકે છે:
- જ્યારે Δ/ 0, ત્યાં 2 વાસ્તવિક મૂળ x 1 = (- બી + √ Δ ) / (2 એ) અને x 2 = (- બી-√ Δ ) / (2 એ) છે .
- જ્યારે Δ = 0, ત્યાં એક રુટ x 1 = x 2 = -b / (2a) હોય છે .
- જ્યારે Δ <0, ત્યાં કોઈ વાસ્તવિક મૂળ નથી, ત્યાં 2 જટિલ મૂળ છે:
x 1 = (- b + i√ -Δ ) / (2 એ) અને x 2 = (- બાય -Δ ) / (2 એ) .
સમસ્યા # 1
3 x 2 +5 x +2 = 0
ઉકેલો:
a = 3, b = 5, c = 2
x 1,2 = (-5 ± √ (5 2 - 4 × 3 × 2)) / (2 × 3) = (-5 ± √ (25-24)) / 6 = (-5 ± 1) / 6
x 1 = (-5 + 1) / 6 = -4/6 = -2/3
x 2 = (-5 - 1) / 6 = -6/6 = -1
સમસ્યા # 2
3 x 2 -6 x +3 = 0
ઉકેલો:
a = 3, b = -6, c = 3
x 1,2 = (6 ± √ ((-6) 2 - 4 × 3 × 3)) / (2 × 3) = (6 ± √ (36-36)) / 6 = (6 ± 0) / 6
x 1 = x 2 = 1
સમસ્યા # 3
x 2 +2 x +5 = 0
ઉકેલો:
a = 1, b = 2, c = 5
x 1,2 = (-2 ± √ (2 2 - 4 × 1 × 5)) / (2 × 1) = (-2 ± √ (4-20)) / 2 = (-2 ± √ (-16 )) / 2
ત્યાં કોઈ વાસ્તવિક ઉકેલો નથી. કિંમતો જટિલ સંખ્યાઓ છે:
x 1 = -1 + 2 i
x 2 = -1 - 2 i
ક્વોડ્રેટિક ફંક્શન ગ્રાફ
વર્ગાત્મક કાર્ય એ બીજો ક્રમનો બહુકોષીય કાર્ય છે:
f ( x ) = ax 2 + bx + c
ચતુર્ભુજ સમીકરણના ઉકેલો એ ચતુર્ભુજ કાર્યના મૂળ છે, જે એક્સ-અક્ષ સાથેના ચતુર્ભુજ ફંક્શન ગ્રાફના આંતરછેદ બિંદુઓ છે, જ્યારે
f ( x ) = 0
જ્યારે એક્સ-અક્ષ સાથેના ગ્રાફના 2 આંતરછેદ બિંદુઓ હોય છે, ત્યારે ચતુર્ભુજ સમીકરણના 2 ઉકેલો હોય છે.
જ્યારે એક્સ-અક્ષો સાથે ગ્રાફનો 1 આંતરછેદ બિંદુ હોય, ત્યારે ચતુર્ભુજ સમીકરણનો 1 સમાધાન હોય છે.
જ્યારે એક્સ-અક્ષ સાથેના ગ્રાફના કોઈ આંતરછેદ બિંદુઓ નથી, ત્યારે અમને વાસ્તવિક ઉકેલો (અથવા 2 જટિલ ઉકેલો) મળતા નથી.