લોગરીધમ નિયમો

આધાર ખ લઘુગણક સંખ્યાબંધ છે હિમાયતી છે કે આપણે ઊભું કરવાની જરૂર આધાર ઓર્ડર નંબર મેળવવા માટે.

લોગરીધમ વ્યાખ્યા

જ્યારે b ની y ની શક્તિમાં ઉભા કરવામાં આવે છે તે બરાબર x છે:

બી વાય = એક્સ

પછી x નો આધાર બી લ logગરીધમ y ની બરાબર છે:

લ bગ બી ( એક્સ ) = વાય

ઉદાહરણ તરીકે જ્યારે:

2 4 = 16

પછી

લ 2 ગ 2 (16) = 4

ઘાતાંકીય કાર્યના વિપરિત કાર્ય તરીકે લોગરીધમ

લોગરીધમિક ફંક્શન,

y = લ bગ બી ( x )

ઘાતાંકીય કાર્યનું વિપરિત કાર્ય છે,

x = બી વાય

તેથી જો આપણે x (x/ 0) ના લોગરીધમના ઘાતાંકીય કાર્યની ગણતરી કરીએ,

f ( f -1 ( x )) = b લોગ b ( x ) = x

અથવા જો આપણે એક્સના ઘાતાંકીય કાર્યના લોગરીધમની ગણતરી કરીએ,

f -1 ( f ( x )) = લ log ગ બી ( b x ) = x

કુદરતી લોગરીધમ (એલએન)

નેચરલ લોગરીધમ એ બેઝ ઇનો લોગરીધમ છે:

ln ( x ) = લ log ગ e ( x )

જ્યારે ઇ સ્થિર સંખ્યા હોય છે:

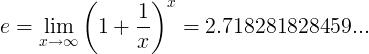
e = \ લિમ_ {x \ રાઇટરો \ ઇન્ફ્ટી} \ ડાબે (1+ \ frac {1} {x} \ અધિકાર) ^ x = 2.718281828459 ...

અથવા

e = \ લિમ_ {x \ રાઇટરો 0} \ ડાબે (1+ \ જમણું x) ^ rac frac {1} {x}

 

જુઓ: પ્રાકૃતિક લોગરીધમ

વ્યસ્ત લોગરીધમ ગણતરી

વ્યસ્ત લોગરીધમ (અથવા વિરોધી લોગરીધમ) ની ગણતરી બેગ બીને લોગરીધમ વાય દ્વારા વધારીને કરવામાં આવે છે:

x = લ log ગ -1 ( વાય ) = બી વાય

લોગરીધમિક ફંક્શન

લોગરીધમિક ફંકશનમાં આનું મૂળ સ્વરૂપ છે:

f ( x ) = લોગ b ( x )

લોગરીધમ નિયમો

નિયમ નામ નિયમ
લોગરીધમ ઉત્પાદન નિયમ
 લોગ બી ( x ∙ y ) = લ bગ બી ( એક્સ ) + લ bગ બી ( વાય )
લોગરીધમ ક્વોન્ટિએન્ટ નિયમ
 લોગ બી ( x / y ) = લોગ બી ( એક્સ ) - લોગ બી ( વાય )
લોગરીધમ પાવર નિયમ
 લ bગ બી ( x વાય ) = વાય ∙ લોગ બી ( એક્સ )
લોગરીધમ આધાર સ્વીચ નિયમ
 લ b ગ બી ( સી ) = 1 / લ log ગ સી ( બી )
લોગરીધમ આધાર પરિવર્તનનો નિયમ
 લોગ બી ( એક્સ ) = લોગ સી ( એક્સ ) / લ log ગ સી ( બી )
લોગરીધમનું વ્યુત્પન્ન
 f ( x ) = લોગ b ( x ) ⇒ f ' ( x ) = 1 / ( x ln ( b ))
લોગરીધમનો ઇન્ટિગ્રલ
 ∫ લોગ ખ ( એક્સ ) ડીએક્સ = x ∙ (લોગ ખ ( એક્સ ) - 1 / LN ( ખ ) ) + સી
નકારાત્મક સંખ્યાનો લોગરીધમ
 લોગ ખ ( એક્સ ) અવ્યાખ્યાયિત છે એક્સ ≤ 0
0 નો લોગરીધમ
 લોગ બી (0) અસ્પષ્ટ છે
\ લિમ_ {x \ થી 0 ^ +} \ ટેક્સ્ટઅપ {લોગ} _ બી (એક્સ) = - \ ઇન્ફટી
Log નો લોગરીધમ
 લ bગ બી (1) = 0
આધારનો લોગરીધમ
 લોગ બી ( બી ) = 1
અનંતનો લોગોરીધમ
 લિમ લોગ b ( x ) = ∞, જ્યારે x → ∞

જુઓ: લોગરીધમ નિયમો

 

લોગરીધમ ઉત્પાદન નિયમ

X અને y ના ગુણાકારનો લોગરીધમ એ x ના લ logગરીધમ અને y ના લોગરીધમનો સરવાળો છે.

લોગ બી ( x ∙ y ) = લ bગ બી ( એક્સ ) + લ bગ બી ( વાય )

દાખ્લા તરીકે:

પ્રવેશ 10 (3 ∙ 7) = પ્રવેશ 10 (3) + પ્રવેશ 10 (7)

લોગરીધમ ક્વોન્ટિએન્ટ નિયમ

X અને y ના ભાગાકારનો લોગરીધમ એ x ના લ logગરીધમ અને y ના લોગરીધમનો તફાવત છે.

લોગ બી ( x / y ) = લોગ બી ( એક્સ ) - લોગ બી ( વાય )

દાખ્લા તરીકે:

પ્રવેશ 10 (3 / 7) = પ્રવેશ 10 (3) - પ્રવેશ 10 (7)

લોગરીધમ પાવર નિયમ

Y ની શક્તિમાં ઉભા કરેલા x નો લોગરીધમ, x ના લarગોરિધમનો y ગણો છે.

લ bગ બી ( x વાય ) = વાય ∙ લોગ બી ( એક્સ )

દાખ્લા તરીકે:

પ્રવેશ 10 (2 8 ) = 8 ∙ પ્રવેશ 10 (2)

લોગરીધમ આધાર સ્વીચ નિયમ

સી નો બેઝ બી લોગરીધમ બી ના બેઝ સી લોગરીધમ દ્વારા વિભાજિત થયેલ છે.

લ b ગ બી ( સી ) = 1 / લ log ગ સી ( બી )

દાખ્લા તરીકે:

લ logગ 2 (8) = 1 / લ logગ 8 (2)

લોગરીધમ આધાર પરિવર્તનનો નિયમ

X નો બેઝ બી લોગરીધમ એ x નો બેઝ સી લોગરીધમ છે જે b ના બેઝ સી લોગરીધમ દ્વારા વહેંચાયેલું છે.

લોગ બી ( એક્સ ) = લોગ સી ( એક્સ ) / લ log ગ સી ( બી )

ઉદાહરણ તરીકે, કેલ્ક્યુલેટરમાં લોગ 2 (8) ની ગણતરી કરવા માટે, આપણે આધારને 10 માં બદલવાની જરૂર છે:

લ logગ 2 (8) = લ logગ 10 (8) / લ logગ 10 (2)

જુઓ: લોગ બેઝ ચેન્જ નિયમ

નકારાત્મક સંખ્યાનો લોગરીધમ

X નો બેઝ બી વાસ્તવિક લarગોરિધમ જ્યારે x <= 0 એ અસ્પષ્ટ હોય ત્યારે x નકારાત્મક અથવા બરાબર શૂન્ય હોય:

x ≤ 0 હોય ત્યારે લ log ગ b ( x ) એ અસ્પષ્ટ હોય છે

જુઓ: નકારાત્મક સંખ્યાનો લોગ

0 નો લોગરીધમ

શૂન્યનો આધાર બી લ logગરીધમ અસ્પષ્ટ છે:

લોગ બી (0) અસ્પષ્ટ છે

X ના આધાર બી લોગરીધમની મર્યાદા, જ્યારે x શૂન્યની નજીક આવે છે, બાદબાકી અનંત છે:

\ લિમ_ {x \ થી 0 ^ +} \ ટેક્સ્ટઅપ {લોગ} _ બી (એક્સ) = - \ ઇન્ફટી

જુઓ: શૂન્યનો લોગ

Log નો લોગરીધમ

એકનો આધાર બી લોગરીધમ શૂન્ય છે:

લ bગ બી (1) = 0

ઉદાહરણ તરીકે, તેહ બેઝ બે લોગરીધમ એક છે શૂન્ય:

લ 2 ગ 2 (1) = 0

જુઓ: એક લોગ

અનંતનો લોગોરીધમ

X ના આધાર બી લોગરીધમની મર્યાદા, જ્યારે x અનંતની નજીક આવે છે:

લિમ લોગ b ( x ) = ∞, જ્યારે x → ∞

જુઓ: અનંતનો લોગ

આધારનો લોગરીધમ

બી નો બેઝ બી લોગરીધમ એક છે:

લોગ બી ( બી ) = 1

ઉદાહરણ તરીકે, બેનો આધાર બે લોગરીધમ એક છે:

લ 2 ગ 2 (2) = 1

લોગરીધમ વ્યુત્પન્ન

ક્યારે

f ( x ) = લોગ b ( x )

પછી f (x) નું વ્યુત્પન્ન:

f ' ( x ) = 1 / ( x ln ( b ))

જુઓ: લોગ વ્યુત્પન્ન

લોગરીધમ અભિન્ન

X ના લોગરીધમનું અભિન્ન

∫ લોગ ખ ( એક્સ ) ડીએક્સ = x ∙ (લોગ ખ ( એક્સ ) - 1 / LN ( ખ ) ) + સી

દાખ્લા તરીકે:

∫ પ્રવેશ 2 ( x ) ડીએક્સ = x ∙ (પ્રવેશ 2 ( x ) - 1 / LN (2) ) + સી

લોગરીધમ આશરે

લ log ગ 2 ( x ) ≈ n + ( x / 2 n - 1),

જટિલ લોગરીધમ

જટિલ સંખ્યા z માટે:

z = રે i re = x + iy

જટિલ લોગરીધમ (n = ...- 2, -1,0,1,2, ...) હશે:

લૉગ z = LN ( R ) + હું ( θ + 2nπ ) = LN (√ ( એક્સ 2 + વાય 2 )) + હું · arctan ( વાય / એક્સ ))

લોગરીધમ સમસ્યાઓ અને જવાબો

સમસ્યા # 1

માટે x શોધો

લ 2 ગ 2 ( x ) + લ 2 ગ 2 ( x -3) = 2

ઉકેલો:

ઉત્પાદનના નિયમનો ઉપયોગ:

પ્રવેશ 2 ( x ∙ ( એક્સ -3)) = 2

લોગરીધમ વ્યાખ્યા અનુસાર લોગરીધમ ફોર્મ બદલવું:

x ∙ ( x -3) = 2 2

અથવા

x 2 -3 x -4 = 0

ચતુર્ભુજ સમીકરણનું સમાધાન:

x 1,2 = [3 ± √ (9 + 16)] / 2 = [3 ± 5] / 2 = 4, -1

નકારાત્મક સંખ્યાઓ માટે લોગરીધમ વ્યાખ્યાયિત નથી, તેથી જવાબ છે:

x = 4

સમસ્યા # 2

માટે x શોધો

પ્રવેશ 3 ( x +2) - લોગ 3 ( x ) = 2

ઉકેલો:

ભાવિ નિયમનો ઉપયોગ:

લ 3 ગ 3 (( x +2) / x ) = 2

લોગરીધમ વ્યાખ્યા અનુસાર લોગરીધમ ફોર્મ બદલવું:

( x +2) / x = 3 2

અથવા

x +2 = 9 x

અથવા

8 x = 2

અથવા

x = 0.25

લોગનો ગ્રાફ (x)

x ના વાસ્તવિક બિન-સકારાત્મક મૂલ્યો માટે લ logગ (એક્સ) વ્યાખ્યાયિત નથી:

લોગરીધમ્સ ટેબલ

x લ x ગ 10 એક્સ લ logગ 2 એક્સ લ logગ ઇ એક્સ
0 અસ્પષ્ટ અસ્પષ્ટ અસ્પષ્ટ
0 + - ∞ - ∞ - ∞
0.0001 -4 -13.287712 -9.210340
0.001 -3 -9.965784 -6.907755
0.01 -2 -6.643856 -4.605170
0.1 -1 -3.321928 -2.302585
1 0 0 0
2 0.301030 1 0.693147
3 0.477121 1.584963 છે 1.098612
4 0.602060 2 1.386294
5 0.698970 2.321928 1.609438
6 0.778151 2.584963 છે 1.791759 છે
7 0.845098 છે 2.807355 છે 1.945910
8 0.903090 3 2.079442
9 0.954243 3.169925 છે 2.197225
10 1 3.321928 2.302585 છે
20 1.301030 4.321928 2.995732 છે
30 1.477121 4.906891 3.401197
40 1.602060 5.321928 68.7988 .887979
50 1.698970 5.643856 છે 3.912023
60 1.778151 5.906991 છે 4.094345
70 1.845098 છે 6.129283 4.248495
80 1.903090 6.321928 4.382027
90 1.954243 6.491853 4.499810
100 2 6.643856 છે 4.605170 છે
200 2.301030 7.643856 છે 5.298317
300 2.477121 8.228819 5.703782 છે
400 2.602060 8.643856 છે 5.991465 છે
500 2.698970 8.965784 છે 6.214608
600 2.778151 9.228819 6.396930
700 2.845098 છે 9.451211 6.551080 છે
800 2.903090 9.643856 છે 6.684612 પર રાખવામાં આવી છે
900 2.954243 9.813781 6.802395
1000 3 9.965784 છે 6.907755 છે
10000 છે 4 13.287712 9.210340

 

લોગરીધમ કેલ્ક્યુલેટર ►

 

આ પણ જુઓ

એલ્જેબ્રા
ઝડપી ટેબલ્સ