અભિન્ન

એકીકરણ એ વ્યુત્પત્તિનું વિપરીત ઓપરેશન છે.

ફંક્શનનો ઇન્ટિગ્રલ એ ફંક્શનના ગ્રાફ હેઠળનો વિસ્તાર છે.

અનિશ્ચિત ઇન્ટિગ્રલ વ્યાખ્યા

ક્યારે dF (x) / dx = f (x) =/ અભિન્ન (f (x) * dx) = F (x) + c

અનિશ્ચિત સંકલન ગુણધર્મો

અભિન્ન (f (x) + g (x)) * dx = અભિન્ન (f (x) * dx) + અભિન્ન (g (x) * dx)

અભિન્ન (a * f (x) * dx) = a * અભિન્ન (f (x) * dx)

અભિન્ન (f (a * x) * dx) = 1 / a * F (a * x) + c

અભિન્ન (f (x + b) * dx) = F (x + b) + c

અભિન્ન (f (a * x + b) * dx) = 1 / a * F (a * x + b) + c

અભિન્ન (df (x) / dx * dx) = f (x)

ઇન્ટિગ્રેશન વેરિયેબલનું પરિવર્તન

ક્યારેx = g (t) અનેડીએક્સ = જી '(ટી) * તા

અભિન્ન (f (x) * dx) = અભિન્ન (f (g (t)) * g '(t) * dt)

ભાગો દ્વારા એકત્રિકરણ

અભિન્ન (f (x) * g '(x) * dx) = f (x) * g (x) - અભિન્ન (f' (x) * g (x) * dx)

ઇન્ટિગ્રેલ્સ ટેબલ

અભિન્ન (f (x) * dx = F (x) + c

અભિન્ન (a * dx) = a * x + c

ઇન્ટિગ્રલ (x ^ n * dx) = 1 / (a ​​+ 1) * x ^ (a + 1) + સી, જ્યારે </ - 1

અભિન્ન (1 / x * dx) = ln (એબીએસ (એક્સ)) + સી

અભિન્ન (e ^ x * dx) = e ^ x + c

અભિન્ન (a ^ x * dx) = a ^ x / ln (x) + c

અભિન્ન (ln (x) * dx) = x * ln (x) - x + c

અભિન્ન (sin (x) * dx) = -cos (x) + c

ઇન્ટિગ્રલ (કોસ (એક્સ) * ડીએક્સ) = સિન (એક્સ) + સી

અભિન્ન (તન (x) * dx) = -ln (એબીએસ (કોસ (એક્સ))) + સી

ઇન્ટિગ્રલ (આર્ક્સિન (એક્સ) * ડીએક્સ) = એક્સ * આર્ક્સિન (એક્સ) + ચોરસ (1-x ^ 2) + સી

ઇન્ટિગ્રલ (આર્કોકોસ (એક્સ) * ડીએક્સ) = એક્સ * આર્કોકોસ (એક્સ) - સ્ક્વેર (1-x ^ 2) + સી

અભિન્ન (આર્ક્ટન (x) * dx) = x * આર્ક્ટન (x) - 1/2 * LN (1 + x ^ 2) + સી

અભિન્ન (dx / (ax + b)) = 1 / a * ln (એબીએસ (એ * x + બી)) + સી

અભિન્ન (1 / sqrt (a ^ 2-x ^ 2) * dx) = આર્ક્સિન (x / a) + સી

અભિન્ન (1 / sqrt (x ^ 2 + - a ^ 2) * dx) = ln (એબીએસ (x + sqrt (x ^ 2 + - a ^ 2)) + સી

અભિન્ન (x * sqrt (x ^ 2-a ^ 2) * dx) = 1 / (a ​​* આર્કોકોસ (x / a)) + સી

અભિન્ન (1 / (a ​​^ 2 + x ^ 2) * dx) = 1 / a * આર્ક્ટન (x / a) + સી

અભિન્ન (1 / (a ​​^ 2-x ^ 2) * dx) = 1 / 2a * ln (એબીએસ (((a + x) / (કુહાડો)))) + સી

અભિન્ન (sinh (x) * dx) = cosh (x) + c

ઇન્ટિગ્રલ (કોશ (એક્સ) * ડીએક્સ) = સિન્હ (એક્સ) + સી

અભિન્ન (તન્હ (x) * dx) = ln (કોશ (x)) + સી

 

ડેફિનેટ ઇન્ટિગ્રલ ડેફિનેશન

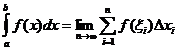
અભિન્ન (a..b, f (x) * dx) = lim (n-/ inf, રકમ (i = 1..n, f (z (i)) * dx (i)) 

ક્યારેx0 = એ, એક્સએન = બી

ડીએક્સ (કે) = એક્સ (કે) - એક્સ (કે -1)

x (k-1) <= z (k) <= x (કે)

ડેફિનેટ ઇન્ટિગલ ગણતરી

ક્યારે ,

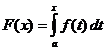 dF (x) / dx = f (x) અને

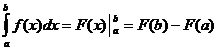
અભિન્ન (a..b, f (x) * dx) = F (b) - F (a) 

ડેફિનેટ ઇન્ટિગલ ગુણધર્મો

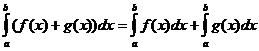
અભિન્ન (a..b, (f (x) + g (x)) * dx) = અભિન્ન (a..b, f (x) * dx) + અભિન્ન (a..b, g (x) * dx )

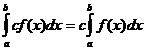
અભિન્ન (a..b, c * f (x) * dx) = c * અભિન્ન (a..b, f (x) * dx)

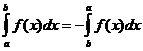
અભિન્ન (a..b, f (x) * dx) = - અભિન્ન (b..a, f (x) * dx)

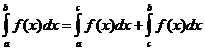
અભિન્ન (a..b, f (x) * dx) = અભિન્ન (a..c, f (x) * dx) + અભિન્ન (c..b, f (x) * dx)

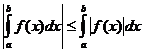
એબીએસ (અવિભાજ્ય (a..b, f (x) * dx)) <= અભિન્ન (a..b, એબીએસ (f (x)) * dx)

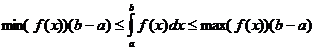મિનિટ (એફ (એક્સ)) * (બા) <= ઇન્ટિગ્રલ (એ..બી, એફ (x) * dx) <= મેક્સ (એફ (એક્સ)) * (બા) ક્યારે[એ, બી] ના x સદસ્ય

ઇન્ટિગ્રેશન વેરિયેબલનું પરિવર્તન

ક્યારેx = g (t) ,ડીએક્સ = જી '(ટી) * તા ,જી (આલ્ફા) = એ ,g (બીટા) = બી

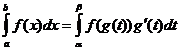
અભિન્ન (a..b, f (x) * dx) = અભિન્ન (આલ્ફા..બેતા, f (g (t)) * g '(t) * dt)

ભાગો દ્વારા એકત્રિકરણ

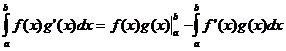
અભિન્ન (a..b, f (x) * g '(x) * dx) = અભિન્ન (a..b, f (x) * g (x) * dx) - અભિન્ન (a..b, f') (x) * g (x) * dx)

મીન મૂલ્ય પ્રમેય

જ્યારે f ( x ) સતત હોય ત્યારે ત્યાં એક બિંદુ હોય છેc એ [એ, બી] નો સભ્ય છે તેથી

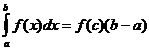
અભિન્ન (a..b, f (x) * dx) = f (c) * (બા)  

ડેફિનેટ ઇન્ટિગલનું ટ્રેપેઝોઇડલ અંદાજ

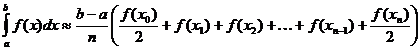
અભિન્ન (a..b, f (x) * dx) ~ (બા) / n * (f (x (0)) / 2 + f (x (1)) + f (x (2)) + .. . + f (x (n-1)) + f (x (n)) / 2)

ગામા કાર્ય

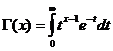
ગામા (x) = અભિન્ન (0..inf, t ^ (x-1) * e ^ (- t) * તા.

X/ 0 માટે ગામા ફંક્શન કન્વર્જન્ટ છે .

ગામા કાર્ય ગુણધર્મો

જી ( x +1) = x જી ( x )

જી ( એન +1) = એન ! , જ્યારે n ℕ (સકારાત્મક પૂર્ણાંક).ના સભ્ય છે

બીટા ફંક્શન

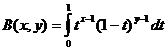
બી (એક્સ, વાય) = અવિભાજ્ય (0..1, ટી ^ (એન-1) * (1-ટી) ^ (વાય -1) * તા.

બીટા ફંક્શન અને ગામા ફંક્શન રિલેશન

બી (એક્સ, વાય) = ગામા (એક્સ) * ગામા (વાય) / ગામા (x + વાય)

 

 

 

કેલ્ક્યુલસ
ઝડપી ટેબલ્સ