ફિબોનાકી નંબર્સ અને સિક્વન્સ
ફિબોનાકી સિક્વન્સ એ સંખ્યાઓનો ક્રમ છે, જ્યાં પ્રત્યેક સંખ્યા 0 અને 1 ની પહેલા બે નંબરો સિવાય 2 અગાઉના સંખ્યાઓનો સરવાળો છે.
- ફિબોનાકી સિક્વન્સ ફોર્મ્યુલા
- ગોલ્ડન રેશિયો કન્વર્ઝન
- ફિબોનાકી સિક્વન્સ ટેબલ
- ફિબોનાકી સિક્વન્સ કેલ્ક્યુલેટર
- સી ++ ફિબોનાકી ફંક્શનનો કોડ
ફિબોનાકી સિક્વન્સ ફોર્મ્યુલા
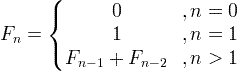
દાખ્લા તરીકે:
એફ 0 = 0
એફ 1 = 1
એફ 2 = એફ 1 + એફ 0 = 1 + 0 = 1
એફ 3 = એફ 2 + એફ 1 = 1 + 1 = 2
એફ 4 = એફ 3 + એફ 2 = 2 + 1 = 3
એફ 5 = એફ 4 + એફ 3 = 3 + 2 = 5
...
ગોલ્ડન રેશિયો કન્વર્ઝન
બે ક્રમિક ફિબોનાકી નંબરોનો ગુણોત્તર, સુવર્ણ ગુણોત્તરમાં ફેરવાય છે:
![]()
એ સુવર્ણ ગુણોત્તર = (1 + √ 5 ) / 2 ≈ 1.61803399 છે
ફિબોનાકી સિક્વન્સ ટેબલ
| એન | એફ એન |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 1 |
| 3 | 2 |
| 4 | 3 |
| 5 | 5 |
| 6 | 8 |
| 7 | 13 |
| 8 | 21 |
| 9 | 34 |
| 10 | 55 |
| 11 | 89 |
| 12 | 144 |
| 13 | 233 |
| 14 | 377 |
| 15 | 610 |
| 16 | 987 |
| 17 | 1597 પર રાખવામાં આવી છે |
| 18 | 2584 |
| 19 | 4181 પર રાખવામાં આવી છે |
| 20 | 6765 |
ફિબોનાકી સિક્વન્સ કેલ્ક્યુલેટર
ટીબીડી
ફિબોનાકી ફંક્શનનો સી કોડ
double Fibonacci(unsigned int n)
{
double f_n =n;
double f_n1=0.0;
double f_n2=1.0;
if( n / 1 ) {
for(int k=2; k<=n; k++) {
f_n = f_n1 + f_n2;
f_n2 = f_n1;
f_n1 = f_n;
}
}
return f_n;
}