ઘાતક નિયમો

ઘાતક નિયમો, ઘાતાકનાં કાયદા અને ઉદાહરણો.

ઘાતક એટલે શું

N ની શક્તિ માટે ઉભા કરેલા આધાર એ, એન વખતના ગુણાકારની બરાબર છે:

a n = a × a × ... × એ

                    n વખત

a એ આધાર છે અને n એ ઘાતાંક છે.

ઉદાહરણો

3 1 = 3

3 2 = 3 × 3 = 9

3 3 = 3 × 3 × 3 = 27

3 4 = 3 × 3 × 3 × 3 = 81

3 5 = 3 × 3 × 3 × 3 × 3 = 243

ખાતાના નિયમો અને ગુણધર્મો

નિયમ નામ નિયમ ઉદાહરણ
ઉત્પાદન નિયમો a n ⋅ a m = a n + m 2 3 ⋅ 2 4 = 2 3 + 4 = 128
a n ⋅ b n = ( a ⋅ b ) n 3 2 ⋅ 4 2 = (3⋅4) 2 = 144
ઉત્તમ નિયમો a n / a m = a n - m 2 5 /2 3 = 2 5-3 = 4
a n / b n = ( a / b ) n 4 3 /2 3 = (4/2) 3 = 8
પાવર નિયમો ( b n ) m = b n⋅m (2 3 ) 2 = 2 3⋅2 = 64
બી એન એમ = બી ( એન એમ ) 2 3 2 = 2 ( 3 2 ) = 512
મી √ ( બી એન ) = બી એન / એમ 2 √ (2 6 ) = 2 6/2 = 8
બી 1 / એન = એન √ બી 8 1/3 = 3 √ 8 = 2
નકારાત્મક ખાવું બી- એન = 1 / બી એન 2 -3 = 1/2 3 = 0.125
શૂન્ય નિયમો બી 0 = 1 5 0 = 1
0 એન = 0, એન / 0 માટે 0 5 = 0
એક નિયમ બી 1 = બી 5 1 = 5
1 એન = 1 1 5 = 1
માઇનસ એક નિયમ 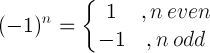(-1) 5 = -1
વ્યુત્પન્ન નિયમ ( x n ) ' = n ⋅ x n -1 ( x 3 ) ' = 3⋅ x 3-1
અભિન્ન નિયમ ∫ x n dx = x n +1 / ( n +1) + C ∫ x 2 dx = x 2 + 1 / (2 + 1) + સી

ઘાનાના ઉત્પાદનના નિયમો

સમાન આધાર સાથે ઉત્પાદનનો નિયમ

a n ⋅ a m = a n + m

ઉદાહરણ:

2 3 ⋅ 2 4 = 2 3 + 4 = 2 7 = 2⋅2⋅2⋅2⋅2⋅2⋅2 = 128

સમાન ઘાતાંકવાળા ઉત્પાદનનો નિયમ

a n ⋅ b n = ( a ⋅ b ) n

ઉદાહરણ:

3 2 ⋅ 4 2 = (3⋅4) 2 = 12 2 = 12⋅12 = 144

જુઓ: મલ્ટિપ્લાઇંગ એક્સ્પેન્સર્સ

એક્સપોનન્ટ્સ યોગ્ય નિયમો

સમાન આધાર સાથે સુસંગત નિયમ

a n / a m = a n - m

ઉદાહરણ:

2 5 /2 3 = 2 5-3 = 2 2 = 2⋅2 = 4

સમાન ઘાતાંકવાળા ક્વોન્ટિએન્ટ નિયમ

a n / b n = ( a / b ) n

ઉદાહરણ:

4 3 /2 3 = (4/2) 3 = 2 3 = 2⋅2⋅2 = 8

જુઓ: ભાગલા પાડનારાઓ

એક્સ્પેન્ટર્સ પાવર નિયમો

પાવર નિયમ I

( a n ) m = a n⋅m

ઉદાહરણ:

(2 3 ) 2 = 2 3⋅2 = 2 6 = 2⋅2⋅2⋅2⋅2⋅2 = 64

પાવર નિયમ II

a n m = a ( n m )

ઉદાહરણ:

2 3 2 = 2 (3 2 ) = 2 (3⋅3) = 2 9 = 2⋅2⋅2⋅2⋅2⋅2⋅2⋅2⋅2 = 512

ર radડિકલ્સ સાથે પાવર શાસન

મી √ ( એ એન ) = એ એન / એમ

ઉદાહરણ:

2 √ (2 6 ) = 2 6/2 = 2 3 = 2⋅2⋅2 = 8

નકારાત્મક ઘાતકી શાસન

બી- એન = 1 / બી એન

ઉદાહરણ:

2 -3 = 1/2 3 = 1 / (2⋅2⋅2) = 1/8 = 0.125

જુઓ: નકારાત્મક ઘાતરો

 

ઘાતક કેલ્ક્યુલેટર ►

 

આ પણ જુઓ

સંખ્યાઓ
ઝડપી ટેબલ્સ