શૂન્ય નંબર (0)
શૂન્ય નંબર વ્યાખ્યા
શૂન્ય કોઈ સંખ્યા અથવા નલ જથ્થાને વર્ણવવા ગણિતમાં વપરાયેલ એક નંબર છે.
જ્યારે ટેબલ પર 2 સફરજન હોય છે અને અમે 2 સફરજન લઈએ છીએ, ત્યારે આપણે કહી શકીએ છીએ કે ટેબલ પર શૂન્ય સફરજન છે.
શૂન્ય નંબર સકારાત્મક સંખ્યા નથી અને નકારાત્મક સંખ્યા નથી.
શૂન્ય એ અન્ય સંખ્યામાં પ્લેસહોલ્ડર અંક પણ છે (દા.ત.: 40,103, 170)
શૂન્ય એક નંબર છે?
શૂન્ય એક નંબર છે. તે સકારાત્મક કે નકારાત્મક સંખ્યા નથી.
શૂન્ય અંક
નંબરો લખતી વખતે શૂન્ય અંકનો ઉપયોગ પ્લેસહોલ્ડર તરીકે થાય છે.
દાખ્લા તરીકે:
204 = 2 × 100 + 0 × 10 + 4 × 1
શૂન્ય નંબરનો ઇતિહાસ
શૂન્ય નંબરની શોધ કોણે કરી?
આધુનિક 0 પ્રતીકની શોધ 6 મી સદીમાં ભારતમાં કરવામાં આવી હતી, જેનો ઉપયોગ પછીથી પર્સિયન અને આરબો અને પછી યુરોપમાં થતો હતો.
શૂન્યનું પ્રતીક
શૂન્ય નંબર 0 ચિન્હ સાથે સૂચવવામાં આવે છે .
અરબી અંકો સિસ્ટમ system પ્રતીકનો ઉપયોગ કરે છે.
શૂન્ય નંબર ગુણધર્મો
x કોઈપણ સંખ્યાને રજૂ કરે છે.
| ઓપરેશન | નિયમ | ઉદાહરણ |
|---|---|---|
ઉમેરો |
x + 0 = x |
3 + 0 = 3 |
બાદબાકી |
x - 0 = x |
3 - 0 = 3 |
ગુણાકાર |
x × 0 = 0 |
5 × 0 = 0 |
વિભાગ |
0 ÷ x = 0 , જ્યારે x ≠ 0 |
0 ÷ 5 = 0 |
| x ÷ 0 અસ્પષ્ટ છે |
5 ÷ 0 અસ્પષ્ટ છે |
|
વિસ્ફોટ |
0 x = 0 |
0 5 = 0 |
| x 0 = 1 |
5 0 = 1 |
|
રુટ |
. 0 = 0 |
|
લોગરીધમ |
લોગ બી (0) અસ્પષ્ટ છે |
|
| |
||
પરિબળ |
0! = 1 |
|
સાઇન |
sin 0º = 0 |
|
કોઝિન |
કોસ 0º = 1 |
|
ટેન્જેન્ટ |
ટેન 0º = 0 |
|
વ્યુત્પન્ન |
0 '= 0 |
|
અભિન્ન |
∫ 0 ડી x = 0 + સે |
|
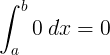 |
શૂન્ય ઉમેરો
સંખ્યા વત્તા શૂન્યનો ઉમેરો સંખ્યા સમાન છે:
x + 0 = x
દાખ્લા તરીકે:
5 + 0 = 5
શૂન્ય બાદબાકી
સંખ્યા બાદબાકી શૂન્યનું બાદબાકી એ સંખ્યાની બરાબર છે:
x - 0 = x
દાખ્લા તરીકે:
5 - 0 = 5
શૂન્ય દ્વારા ગુણાકાર
સંખ્યા ગુણ્યા શૂન્યનું ગુણાકાર શૂન્ય બરાબર છે:
x × 0 = 0
દાખ્લા તરીકે:
5 × 0 = 0
સંખ્યા શૂન્ય દ્વારા વિભાજિત
શૂન્ય દ્વારા સંખ્યાના ભાગની વ્યાખ્યા નથી:
x ÷ 0 અસ્પષ્ટ છે
દાખ્લા તરીકે:
5 ÷ 0 અસ્પષ્ટ છે
શૂન્ય સંખ્યા દ્વારા વિભાજિત
કોઈ સંખ્યા દ્વારા શૂન્યનું વિભાજન શૂન્ય છે:
0 ÷ x = 0
દાખ્લા તરીકે:
0 ÷ 5 = 0
શૂન્ય શક્તિ માટે સંખ્યા
શૂન્ય દ્વારા વધારવામાં આવેલી સંખ્યાની શક્તિ એક છે:
x 0 = 1
દાખ્લા તરીકે:
5 0 = 1
શૂન્યનો લોગરીધમ
શૂન્યનો આધાર બી લ logગરીધમ અસ્પષ્ટ છે:
લોગ બી (0) અસ્પષ્ટ છે
ત્યાં કોઈ સંખ્યા નથી કે આપણે શૂન્ય મેળવવા માટે આધાર બી વધારી શકીએ.
જ્યારે x બેઝ બી લોગરીધમની મર્યાદા, જ્યારે x શૂન્ય ફેરવે છે તે માઇનસ અનંત છે:
![]()
સમૂહો કે જેમાં શૂન્ય છે
શૂન્ય એ કુદરતી નંબરો, પૂર્ણાંકોની સંખ્યા, વાસ્તવિક સંખ્યાઓ અને જટિલ નંબરો સમૂહનું એક તત્વ છે:
| સેટ | સભ્યપદ સંકેત સેટ કરો |
|---|---|
| પ્રાકૃતિક સંખ્યા (નકારાત્મક) | 0 ∈ ℕ 0 |
| પૂર્ણાંક સંખ્યા | 0 ∈ ℤ |
| વાસ્તવિક સંખ્યાઓ | 0 ∈ ℝ |
| જટિલ સંખ્યાઓ | 0 ∈ ℂ |
| તર્કસંગત નંબરો | 0 ∈ ℚ |
શૂન્ય બરાબર કે વિચિત્ર નંબર છે?
સમાન સંખ્યાઓનો સમૂહ છે:
{..., -10, -8, -6, -4, -2, 0, 2, 4, 6, 8, 10, ...}
વિચિત્ર સંખ્યાઓનો સમૂહ છે:
{..., -9, -7, -5, -3, -1, 1, 3, 5, 7, 9, ...}
શૂન્ય એ પૂર્ણાંક 2 ની પૂર્ણાંક છે:
0 × 2 = 0
શૂન્ય એ સેટ કરેલી સમાન સંખ્યાના સભ્ય છે:
0 ∈ {2 કે , કે ∈ℤ}
તેથી શૂન્ય એક સમાન સંખ્યા છે, વિચિત્ર સંખ્યા નથી.
શૂન્ય એક કુદરતી સંખ્યા છે?
કુદરતી નંબરો સેટ માટે બે વ્યાખ્યાઓ છે.
બિન નકારાત્મક પૂર્ણાંકોનો સમૂહ:
ℕ 0 = {0,1,2,3,4,5,6,7,8, ...}
સકારાત્મક પૂર્ણાંકોનો સમૂહ:
ℕ 1 = {1,2,3,4,5,6,7,8, ...}
ઝીરો બિન નકારાત્મક પૂર્ણાંકોના સમૂહનો સભ્ય છે:
0 ∈ ℕ 0
શૂન્ય એ સકારાત્મક પૂર્ણાંકોના સેટનો સભ્ય નથી:
0 ∉ ℕ 1
શૂન્ય એક સંપૂર્ણ સંખ્યા છે?
સંપૂર્ણ સંખ્યા માટે ત્રણ વ્યાખ્યા છે:
પૂર્ણાંક નંબરોનો સમૂહ:
ℤ = {0,1,2,3,4,5,6,7,8, ...}
બિન નકારાત્મક પૂર્ણાંકોનો સમૂહ:
ℕ 0 = {0,1,2,3,4,5,6,7,8, ...}
સકારાત્મક પૂર્ણાંકોનો સમૂહ:
ℕ 1 = {1,2,3,4,5,6,7,8, ...}
શૂન્ય એ પૂર્ણાંક નંબરો અને બિન નકારાત્મક પૂર્ણાંકોના સમૂહનો સભ્ય છે:
0 ∈ ℤ
0 ∈ ℕ 0
શૂન્ય એ સકારાત્મક પૂર્ણાંકોના સેટનો સભ્ય નથી:
0 ∉ ℕ 1
શું શૂન્ય પૂર્ણાંક નંબર છે?
પૂર્ણાંક નંબરોનો સમૂહ:
ℤ = {0,1,2,3,4,5,6,7,8, ...}
શૂન્ય એ પૂર્ણાંક નંબરોના સમૂહનો સભ્ય છે:
0 ∈ ℤ
તો શૂન્ય એ પૂર્ણાંક નંબર છે.
શૂન્ય એક તર્કસંગત નંબર છે?
બુદ્ધિગમ્ય સંખ્યા એ એવી સંખ્યા છે જે બે પૂર્ણાંક નંબરોના ભાગ તરીકે વ્યક્ત કરી શકાય છે:
ℚ = { n / મી ; એન , એમ ∈ℤ}
શૂન્ય બે પૂર્ણાંક નંબરોના ભાગ તરીકે લખી શકાય છે.
દાખ્લા તરીકે:
0 = 0/3
તેથી શૂન્ય એક બુદ્ધિગમ્ય સંખ્યા છે.
શૂન્ય એ સકારાત્મક સંખ્યા છે?
સકારાત્મક સંખ્યાને એવી સંખ્યા તરીકે વ્યાખ્યાયિત કરવામાં આવે છે જે શૂન્યથી મોટી હોય:
x / 0
દાખ્લા તરીકે:
5/ 0
શૂન્ય શૂન્ય કરતા વધારે ન હોવાથી, તે સકારાત્મક સંખ્યા નથી.
શૂન્ય એક મુખ્ય નંબર છે?
સંખ્યા 0 એ મુખ્ય સંખ્યા નથી.
શૂન્ય એ સકારાત્મક સંખ્યા નથી અને તેમાં સંખ્યાબંધ વિભાગો છે.
સૌથી ઓછી સંખ્યા 2 છે.