בית / מתמטיקה / הסתברות /שונות

שׁוֹנוּת

בהסתברות ובסטטיסטיקה השונות של משתנה אקראי היא הערך הממוצע של המרחק הריבועי מהערך הממוצע. זה מייצג את האופן שבו המשתנה האקראי מתפזר בסמוך לערך הממוצע. שונות קטנה מציינת כי המשתנה האקראי מופץ בסמוך לערך הממוצע. שונות גדולה מצביעה על כך שהמשתנה האקראי מופץ רחוק מהערך הממוצע. לדוגמא, בהתפלגות נורמלית, עקומת פעמון צרה תהיה בעלת שונות קטנה ועקומת פעמון רחבה תהיה עם שונות גדולה.

הגדרת שונות

השונות של משתנה אקראי X היא הערך הצפוי של ריבועי ההפרש של X והערך הצפוי μ.

σ ² = Var ( X ) = E [( X - μ ) ² ]

מהגדרת השונות שנוכל לקבל

σ ² = Var ( X ) = E ( X ² ) - μ ²

שונות של משתנה אקראי רציף

למשתנה אקראי רציף עם ערך ממוצע μ ופונקציית צפיפות הסתברות f (x):

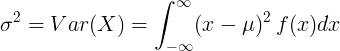
$\ sigma ^ 2 = Var (X) = \ int _ {- \ infty} ^ {\ infty} (x- \ mu) ^ 2 \: f (x) dx$

או

$Var (X) = \ left [\ int _ {- \ infty} ^ {\ infty} x ^ 2 \: f (x) dx \ right] - \ mu ^ 2$

שונות של משתנה אקראי בדיד

עבור משתנה אקראי נפרד X עם ערך ממוצע μ ופונקציית מסת הסתברות P (x):

$\ sigma ^ 2 = Var (X) = \ sum_ {i} ^ {} (x_i- \ mu _X) ^ 2P_X (x_i)$

או

$Var (X) = \ שמאל [\ sum_ {i} ^ {} x_i ^ 2P (x_i) \ ימין] - \ mu ^ 2$

מאפייני שונות

כאשר X ו- Y הם משתנים אקראיים עצמאיים:

Var ( X + Y ) = Var ( X ) + Var ( Y )

סטיית תקן ►

ראה גם

סבירות וסטטיסטיקה

שולחנות מהירים