בית / מתמטיקה / הסתברות /סטיית תקן

סטיית תקן

בהסתברות ובסטטיסטיקה סטיית התקן של משתנה אקראי היא המרחק הממוצע של משתנה אקראי מהערך הממוצע.

הוא מייצג את אופן הפצת המשתנה האקראי בסמוך לערך הממוצע. סטיית תקן קטנה מציינת כי המשתנה האקראי מופץ בסמוך לערך הממוצע. סטיית תקן גדולה מצביעה על כך שהמשתנה האקראי מופץ רחוק מהערך הממוצע.

נוסחת הגדרת סטיית תקן

סטיית התקן היא השורש הריבועי של השונות של משתנה אקראי X, עם הערך הממוצע של μ.

$\ sigma = std (X) = \ sqrt {Var (X)} = \ sqrt {E ((X- \ mu) ^ 2}$

מהגדרת סטיית התקן שנוכל לקבל

$\ sigma = std (X) = \ sqrt {E (X ^ 2) - \ mu ^ 2}$

סטיית תקן של משתנה אקראי רציף

למשתנה אקראי רציף עם ערך ממוצע μ ופונקציית צפיפות הסתברות f (x):

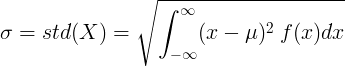
$\ sigma = std (X) = \ sqrt {\ int _ {- \ infty} ^ {\ infty} (x- \ mu) ^ 2 \: f (x) dx}$

או

$\ sigma = std (X) = \ sqrt {\ left [\ int _ {- \ infty} ^ {\ infty} x ^ 2 \: f (x) dx \ right] - \ mu ^ 2}$

סטיית תקן של משתנה אקראי בדיד

עבור משתנה אקראי נפרד X עם ערך ממוצע μ ופונקציית מסת הסתברות P (x):

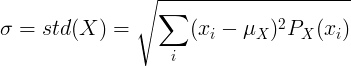
$\ sigma = std (X) = \ sqrt {\ sum_ {i} ^ {} (x_i- \ mu _X) ^ 2P_X (x_i)}$

או

$\ sigma = std (X) = \ sqrt {\ left [\ sum_ {i} ^ {} x_i ^ 2P (x_i) \ right] - \ mu ^ 2}$

חלוקת הסתברות ►

ראה גם

סבירות וסטטיסטיקה

שולחנות מהירים