חלוקת הסתברויות
בהסתברות וסטטיסטיקה התפלגות היא מאפיין של משתנה אקראי, מתאר את ההסתברות של המשתנה האקראי בכל ערך.
לכל התפלגות פונקציה מסוימת של צפיפות הסתברות ופונקציה של חלוקת הסתברות.
למרות שיש מספר בלתי מוגדר של התפלגויות הסתברות, ישנן מספר התפלגויות נפוצות בשימוש.
פונקציית התפלגות מצטברת
התפלגות ההסתברות מתוארת על ידי פונקציית ההתפלגות המצטברת F (x),
המהווה את ההסתברות של משתנה אקראי X לקבל ערך קטן או שווה ל- x:
F ( x ) = P ( X ≤ x )
הפצה רציפה
פונקציית ההתפלגות המצטברת F (x) מחושבת על ידי אינטגרציה של פונקציית צפיפות ההסתברות f (u) של משתנה אקראי רציף X.
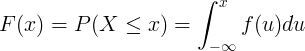
הפצה דיסקרטית
פונקציית ההתפלגות המצטברת F (x) מחושבת על ידי סיכום של פונקציית ההסתברות P (u) של משתנה אקראי בדיד X.
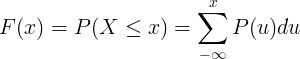
טבלת הפצות רציפה
התפלגות רציפה היא התפלגות של משתנה אקראי רציף.
דוגמא להפצה רציפה
...
טבלת הפצות רציפה
| שם ההפצה | סמל הפצה | פונקציית צפיפות הסתברות (pdf) | מתכוון | שׁוֹנוּת |
|---|---|---|---|---|
| f X ( x ) |
μ = E ( X ) |
σ 2 = Var ( X ) |
||
| רגיל / גאוסי | X ~ N (μ, σ 2 ) |
|
μ | σ 2 |
| מדים | X ~ U ( a , b ) |
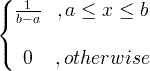 |
|
|
| אקספוננציאלי | X ~ exp (λ) | |
|
|
| גמא | X ~ גמא ( c , λ) | 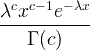 x / 0, c / 0, λ/ 0 |
|
|
| כיכר צ'י | X ~ χ 2 ( k ) |
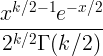 |
k |
2 k |
| וויארט | ||||
| F | X ~ F ( k 1 , k 2 ) |
|||
| בטא | ||||
| וויבול | ||||
| יומן-נורמלי | X ~ LN (μ, σ 2 ) |
|||
| ריילי | ||||
| קושי | ||||
| דיריכלט | ||||
| לפלס | ||||
| לִגבּוֹת | ||||
| אורז | ||||
| תלמיד |
טבלת הפצות דיסקרטיות
התפלגות דיסקרטית היא התפלגות של משתנה אקראי בדיד.
דוגמה להפצה דיסקרטית
...
טבלת הפצות דיסקרטיות
| שם ההפצה | סמל הפצה | פונקציית מסת הסתברות (pmf) | מתכוון | שׁוֹנוּת | |
|---|---|---|---|---|---|
| f x ( k ) = P ( X = k ) k = 0,1,2, ... |
E ( x ) | Var ( x ) | |||
| בינומיאל | X ~ סל ( n , p ) |
|
np |
np (1- p ) |
|
| פואסון | X ~ פואסון (λ) |
|
λ ≥ 0 |
λ |
λ |
| מדים | X ~ U ( a, b ) |
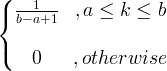 |
|
|
|
| גֵאוֹמֶטרִי | X ~ Geom ( p ) |
|
|
|
|
| היפר-גיאומטרי | X ~ HG ( N , K , n ) |
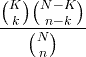 |
N = 0,1,2, ... K = 0,1, .., N n = 0,1, ..., N |
|
|
| ברנולי | X ~ ברן ( p ) |
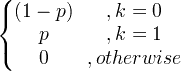 |
p |
p (1- p ) |
|
ראה גם
סבירות וסטטיסטיקה
שולחנות מהירים