अविभाज्य

एकीकरण व्युत्पत्ति का रिवर्स ऑपरेशन है।

एक फ़ंक्शन का इंटीग्रल फ़ंक्शन के ग्राफ़ के तहत क्षेत्र है।

अनिश्चितकालीन अभिन्न परिभाषा

कब dF (x) / dx = f (x) =/ इंटीग्रल (f (x) * dx) = F (x) / c

अनिश्चितकालीन अभिन्न गुण

इंटीग्रल (f (x) + g (x)) * dx = इंटीग्रल (f (x) * dx) + इंटीग्रल (g (x) * dx)

अभिन्न (एक * f (x) * dx) = एक * इंटीग्रल (f (x) * dx)

अभिन्न (f (a * x) * dx) = 1 / a * F (a * x) + c

अभिन्न (f (x + b) * dx) = F (x + b) + c

अभिन्न (f (a * x + b) * dx) = 1 / a * F (a * x + b) + c

अभिन्न (df (x) / dx * dx) = f (x)

एकीकरण चर का परिवर्तन

कबx = g (t) तथाdx = g '(t) * dt

इंटीग्रल (f (x) * dx) = इंटीग्रल (f (g (t)) * g '(t) * dt)

भागों द्वारा एकीकरण

अभिन्न (f (x) * g '(x) * dx) = f (x) * g (x) - इंटीग्रल (f' (x) * g (x) * dx)

इंटीग्रल टेबल

अभिन्न (f (x) * dx = F (x) + c

अभिन्न (एक * dx) = एक * x + c

अभिन्न (x ^ n * dx) = 1 / (a ​​+ 1) * x ^ (a + 1) + c, जब </ - 1

अभिन्न (1 / x * dx) = ln (abs (x)) + c

अभिन्न (ई ^ एक्स * डीएक्स) = ई ^ एक्स + सी

अभिन्न (ए ^ एक्स * डीएक्स) = ए ^ एक्स / एलएन (एक्स) + सी

अभिन्न (ln (x) * dx) = x * ln (x) - x + c

अभिन्न (पाप (x) * dx) = -cos (x) + c

अभिन्न (cos (x) * dx) = sin (x) + c

अभिन्न (tan (x) * dx) = -ln (abs (cos (x))) + c

अभिन्न (आर्क्सिन (x) * dx) = x * आर्क्सिन (x) + sqrt (1-x ^ 2 + + c

अभिन्न (arccos (x) * dx) = x * arccos (x) - sqrt (1-x ^ 2 + + c

इंटीग्रल (आर्कटन (x) * dx) = x * आर्कटन (x) - 1/2 * ln (1 + x ^ 2) + c

अभिन्न (dx / / (ax + b)) = 1 / a * ln (abs (a * x + b)) + c

अभिन्न (1 / sqrt (a ^ 2-x ^ 2) * dx) = आर्क्सिन (x / a) + c

अभिन्न (1 / sqrt (x ^ 2 + - a ^ 2) * dx) = ln (abs (x + sqrt) (x ^ 2 + - a ^ 2)) + c

अभिन्न (x * sqrt (x ^ 2-a ^ 2) * dx) = 1 / (a ​​* arccos (x / a)) + c

अभिन्न (1 / (a ​​^ 2 + x ^ 2) * dx) = 1 / * * आर्कटिक (x / a) c

अभिन्न (1 / (a ​​^ 2-x ^ 2) * dx) = 1 / 2a * ln (abs ((a + x) / (ax)) + c

अभिन्न (sinh (x) * dx) = cosh (x) + c

अभिन्न (कोश (x) * dx) = sinh (x) + c

अभिन्न (tanh (x) * dx) = ln (cosh (x)) + c

 

निश्चित इंटीग्रल परिभाषा;

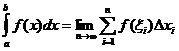
अभिन्न (a..b, f (x) * dx) = lim (n-/ inf, sum (i = 1..n, f (z (i)) * dx (i)) 

कबx0 = a, xn = b

dx (k) = x (k) - x (k-1)

x (k-1) <= z (k) <= x (k)

निश्चित अभिन्न गणना

कब ,

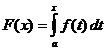 dF (x) / dx = f (x) तथा

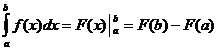
अभिन्न (a..b, f (x) * dx) = F (b) - F (a) 

निश्चित अभिन्न गुण

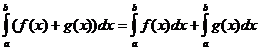
इंटीग्रल (a..b, (f (x) + g (x)) * dx) = इंटीग्रल (a.b, f (x) * dx) + इंटीग्रल (a.b, g (x) * dx )

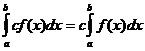
इंटीग्रल (a.b, c * f (x) * dx) = c * इंटीग्रल (a..b, f (x) * dx)

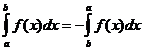
इंटीग्रल (a..b, f (x) * dx) = - इंटीग्रल (b..a, f (x) * dx)

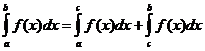
इंटीग्रल (a.b, f (x) * dx) = इंटीग्रल (a..c, f (x) * dx) + इंटीग्रल (c..b, f (x) * dx)

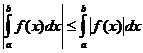
abs (इंटीग्रल (a..b, f (x) * dx)) <= इंटीग्रल (a..b, abs (f (x)) * dx)

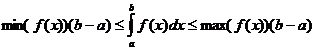min (f (x)) * (ba) <= इंटीग्रल (a..b, f (x) * dx) <= max (f (x)) * (ba) कबx सदस्य [a, b]

एकीकरण चर का परिवर्तन

कबx = g (t) ,dx = g '(t) * dt ,g (अल्फ़ा) = a ,जी (बीटा) = बी

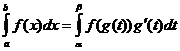
इंटीग्रल (a..b, f (x) * dx) = इंटीग्रल (अल्फा..बीटा, f (g (t)) * g '(t) * dt)

भागों द्वारा एकीकरण

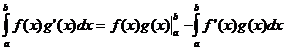
इंटीग्रल (a.b, f (x) * g '(x) * dx) = इंटीग्रल (a..b, f (x) * g (x) * dx) - इंटीग्रल (a..b, f') (x) * g (x) * dx)

मतलब मूल्य प्रमेय

जब f ( x ) निरंतर होता है तो एक बिंदु होता हैc, [a, b] का सदस्य है इसलिए

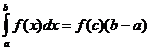
अभिन्न (a..b, f (x) * dx) = f (c) * (ba)  

निश्चित इंटीग्रल का ट्रैपेज़ॉइडल अनुमोदन

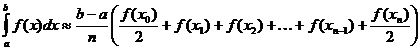
अभिन्न (a..b, f (x) * dx) ~ (ba) / n * (f (x (0)) / 2 + f (x (1)) + f (x (2)) + ।। । + f (x (n-1)) + f (x (n)) / 2)

गामा समारोह

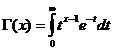
गामा (x) = अभिन्न (0..inf, t ^ (x-1) * e ^ (- t) * dt

गामा फ़ंक्शन x/ 0 के लिए अभिसरण है ।

गामा क्रिया गुण

G ( x +1) = x G ( x )

जी ( एन +1) = एन ! , जब n ℕ (धनात्मक पूर्णांक)।का सदस्य है

बीटा फ़ंक्शन

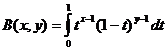
B (x, y) = अभिन्न (0..1, t ^ (n-1) * (1-t) ^ (y-1) * dt

बीटा फंक्शन और गामा फंक्शन रिलेशन

B (x, y) = गामा (x) * गामा (y) / गामा (x + y)

 

 

 

कैलकुलस
रैपिड टाइलें