Kvadratna jednadžba
Kvadratna jednadžba je polinom drugog reda s 3 koeficijenta - a , b , c .
Kvadratna jednadžba dana je:
sjekira 2 + bx + c = 0
Rješenje kvadratne jednadžbe dato je s 2 broja x 1 i x 2 .
Kvadratnu jednadžbu možemo promijeniti u oblik:
( x - x 1 ) ( x - x 2 ) = 0
Kvadratna formula
Rješenje kvadratne jednadžbe daje kvadratna formula:
![]()
Izraz unutar kvadratnog korijena naziva se diskriminantan i označava se s Δ:
Δ = b 2 - 4 ac
Kvadratna formula s diskriminacijskim zapisom:
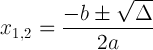
Ovaj je izraz važan jer nam može reći o rješenju:
- Kad je Δ/ 0, postoje 2 stvarna korijena x 1 = (- b + √ Δ ) / (2a) i x 2 = (- b-√ Δ ) / (2a) .
- Kada je Δ = 0, postoji jedan korijen x 1 = x 2 = -b / (2a) .
- Kada je Δ <0, nema pravih korijena, postoje 2 složena korijena:
x 1 = (- b + i√ -Δ ) / (2a) i x 2 = (- bi√ -Δ ) / (2a) .
Problem # 1
3 x 2 +5 x +2 = 0
riješenje:
a = 3, b = 5, c = 2
x 1,2 = (-5 ± √ (5 2 - 4 × 3 × 2)) / (2 × 3) = (-5 ± √ (25-24)) / 6 = (-5 ± 1) / 6
x 1 = (-5 + 1) / 6 = -4/6 = -2/3
x 2 = (-5 - 1) / 6 = -6/6 = -1
Problem # 2
3 x 2 -6 x +3 = 0
riješenje:
a = 3, b = -6, c = 3
x 1,2 = (6 ± √ ((-6) 2 - 4 × 3 × 3)) / (2 × 3) = (6 ± √ (36-36)) / 6 = (6 ± 0) / 6
x 1 = x 2 = 1
Problem # 3
x 2 +2 x +5 = 0
riješenje:
a = 1, b = 2, c = 5
x 1,2 = (-2 ± √ (2 2 - 4 × 1 × 5)) / (2 × 1) = (-2 ± √ (4-20)) / 2 = (-2 ± √ (-16 )) / 2
Pravih rješenja nema. Vrijednosti su složeni brojevi:
x 1 = -1 + 2 i
x 2 = -1 - 2 i
Kvadratni graf funkcije
Kvadratna funkcija je polinomska funkcija drugog reda:
f ( x ) = os 2 + bx + c
Rješenja kvadratne jednadžbe korijeni su kvadratne funkcije, odnosno presjecišta grafa kvadratne funkcije s osi x, kada
f ( x ) = 0
Kada postoje dvije točke presjeka grafa s osi x, postoje 2 rješenja za kvadratnu jednadžbu.
Kada postoji 1 presječna točka grafikona s osi x, postoji 1 rješenje kvadratne jednadžbe.
Kad nema presječnih točaka grafa s osi x, ne dobivamo stvarna rješenja (ili 2 složena rješenja).