Prirodni logaritam - ln (x)
Prirodni logaritam je logaritam baze e broja.
- Definicija prirodnog logaritma (ln)
- Pravila i svojstva prirodnog logaritma (ln)
- Složeni logaritam
- Grafikon ln (x)
- Tablica prirodnih logaritama (ln)
- Kalkulator prirodnog logaritma
Definicija prirodnog logaritma
Kada
e y = x
Tada je osnovni e logaritam x
ln ( x ) = log e ( x ) = y
E konstantna ili Eulerov broj je:
e ≈ 2,71828183
Ln kao inverzna funkcija eksponencijalne funkcije
Funkcija prirodnog logaritma ln (x) je inverzna funkcija eksponencijalne funkcije e x .
Za x/ 0,
f ( f -1 ( x )) = e ln ( x ) = x
Ili
f -1 ( f ( x )) = ln ( e x ) = x
Pravila i svojstva prirodnog logaritma
| Naziv pravila | Pravilo | Primjer |
|---|---|---|
Pravilo proizvoda |
ln ( x ∙ y ) = ln ( x ) + ln ( y ) |
ln (3 ∙ 7) = ln (3) + ln (7) |
Pravilo količnika |
ln ( x / y ) = ln ( x ) - ln ( y ) |
ln (3 / 7) = u (3) - ln (7) |
Pravilo moći |
ln ( x y ) = y ∙ ln ( x ) |
ln (2 8 ) = 8 ∙ ln (2) |
U izvedenici |
f ( x ) = ln ( x ) ⇒ f ' ( x ) = 1 / x | |
U cjelini |
∫ ln ( x ) dx = x ∙ (ln ( x ) - 1) + C | |
ln negativnog broja |
ln ( x ) nije definirano kada je x ≤ 0 | |
nula |
ln (0) nije definirano | |
U jednom |
ln (1) = 0 | |
U beskonačnosti |
lim ln ( x ) = ∞, kada je x → ∞ | |
| Eulerov identitet | ln (-1) = i π |
Pravilo logaritamskog proizvoda
Logaritam množenja x i y zbroj je logaritma x i logaritma y.
log b ( x ∙ y ) = log b ( x ) + log b ( y )
Na primjer:
log 10 (3 ∙ 7) = log 10 (3) + log 10 (7)
Pravilo količnika logaritma
Logaritam dijeljenja x i y je razlika logaritma x i logaritma y.
log b ( x / y ) = log b ( x ) - log b ( y )
Na primjer:
log 10 (3 / 7) = log 10 (3) - log 10 (7)
Pravilo snage logaritma
Logaritam x podignut u potenciju y je y puta logaritam x.
log b ( x y ) = y ∙ log b ( x )
Na primjer:
log 10 (2 8 ) = 8 ∙ log 10 (2)
Derivat prirodnog logaritma
Izvod funkcije prirodnog logaritma je recipročna funkcija.
Kada
f ( x ) = ln ( x )
Izvod f (x) je:
f ' ( x ) = 1 / x
Integral prirodnog logaritma
Integral funkcije prirodnog logaritma dan je:
Kada
f ( x ) = ln ( x )
Integral f (x) je:
∫ f ( x ) dx = ∫ ln ( x ) dx = x ∙ (ln ( x ) - 1) + C
Ln od 0
Prirodni logaritam nule nije definiran:
ln (0) nije definirano
Granica blizu 0 prirodnog logaritma x, kada se x približi nuli, je minus beskonačnost:
![]()
Ln od 1
Prirodni logaritam jedinice jedan je nula:
ln (1) = 0
Ln beskonačnosti
Granica prirodnog logaritma beskonačnosti, kada se x približava beskonačnosti jednaka je beskonačnosti:
lim ln ( x ) = ∞, kada je x → ∞
Složeni logaritam
Za kompleksni broj z:
z = re iθ = x + iy
Složeni logaritam bit će (n = ...- 2, -1,0,1,2, ...):
Log z = ln ( r ) + i ( θ + 2nπ ) = ln (√ ( x 2 + y 2 )) + i · arktan ( y / x ))
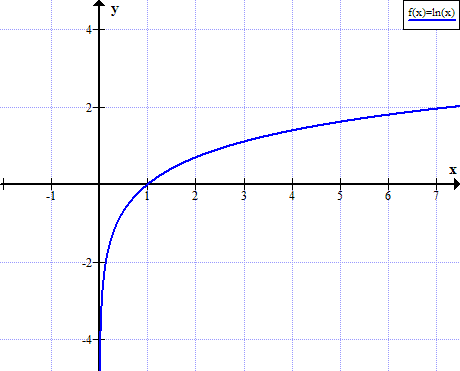
Grafikon ln (x)
ln (x) nije definiran za stvarne pozitivne vrijednosti x:
Tablica prirodnih logaritama
| x | ln x |
|---|---|
| 0 | nedefiniran |
| 0 + | - ∞ |
| 0,0001 | -9,210340 |
| 0,001 | -6,907755 |
| 0,01 | -4.605170 |
| 0,1 | -2.302585 |
| 1 | 0 |
| 2 | 0,693147 |
| e ≈ 2.7183 | 1 |
| 3 | 1.098612 |
| 4 | 1.386294 |
| 5 | 1,609438 |
| 6 | 1.791759 |
| 7 | 1.945910 |
| 8 | 2.079442 |
| 9 | 2.197225 |
| 10 | 2,302585 |
| 20 | 2.995732 |
| 30 | 3,401197 |
| 40 | 3.688879 |
| 50 | 3,912023 |
| 60 | 4.094345 |
| 70 | 4.248495 |
| 80 | 4.382027 |
| 90 | 4,499810 |
| 100 | 4,605170 |
| 200 | 5.298317 |
| 300 | 5,703782 |
| 400 | 5,991465 |
| 500 | 6.214608 |
| 600 | 6,396930 |
| 700 | 6,551080 |
| 800 | 6,684612 |
| 900 | 6,802395 |
| 1000 | 6,907755 |
| 10000 | 9,210340 |
Vidi također
- Logaritam (zapisnik)
- Kalkulator prirodnog logaritma
- Prirodni logaritam nule
- Prirodni logaritam jedinice
- Prirodni logaritam e
- Prirodni logaritam beskonačnosti
- Prirodni logaritam negativnog broja
- Ln inverzna funkcija
- ln (x) graf
- Tablica prirodnog logaritma
- Logaritamski kalkulator
- e konstanta