Konvolucija
Konvolucija je korelacijska funkcija f (τ) s obrnutom funkcijom g (t-τ).
Operator konvolucije simbol je zvjezdice * .
- Neprekidna konvolucija
- Diskretna konvolucija
- 2D diskretna konvolucija
- Filtrirajte implementaciju sa savijanjem
- Teorem o konvoluciji
Neprekidna konvolucija
Konvolacija f (t) i g (t) jednaka je integralu f (τ) puta f (t-τ):
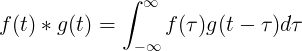
Diskretna konvolucija
Konvolacija 2 diskretne funkcije definirana je kao:
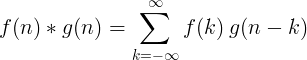
2D diskretna konvolucija
Dvodimenzionalna diskretna konvolucija obično se koristi za obradu slike.
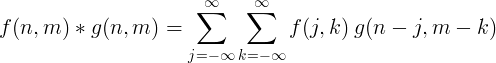
Filtrirajte implementaciju sa savijanjem
Diskretni ulazni signal x (n) možemo filtrirati konvolucijom s impulsnim odzivom h (n) da bismo dobili izlazni signal y (n).
y ( n ) = x ( n ) * h ( n )
Teorem o konvoluciji
Fourierova transformacija množenja 2 funkcije jednaka je konvoluciji Fourierovih transformacija svake funkcije:
ℱ { f ⋅ g } = ℱ { f } * ℱ { g }
Fourierova transformacija konvolucije 2 funkcije jednaka je množenju Fourierovih transformacija svake funkcije:
ℱ { f * g } = ℱ { f } ⋅ ℱ { g }
Teorem o konvoluciji za kontinuiranu Fourierovu transformaciju
ℱ { f ( t ) ⋅ g ( t )} = ℱ { f ( t )} * ℱ { g ( t )} = F ( ω ) * G ( ω )
ℱ { f ( t ) * g ( t )} = ℱ { f ( t )} ⋅ ℱ { g ( t )} = F ( ω ) ⋅ G ( ω )
Teorem o konvoluciji za diskretnu Fourierovu transformaciju
ℱ { f ( n ) ⋅ g ( n )} = ℱ { f ( n )} * ℱ { g ( n )} = F ( k ) * G ( k )
ℱ { f ( n ) * g ( n )} = ℱ { f ( n )} ⋅ ℱ { g ( n )} = F ( k ) ⋅ G ( k )
Teorem o konvoluciji za Laplaceovu transformaciju
ℒ { f ( t ) * g ( t )} = ℒ { f ( t )} ⋅ ℒ { g ( t )} = F ( s ) ⋅ G ( s )
Vidi također
RAČUN
- Ograničiti
- Izvedena
- Sastavni
- Niz
- Laplaceova transformacija
- Konvolucija
- Simboli računa
BRZE TABLICE